算法总结笔记.md
算法总结笔记
[toc]
第一章 回溯算法 DFS(深度优先搜索)
算法框架
for 选择 in 选择列表:
# 做选择
将该选择从选择列表移除
路径.add(选择)
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
将该选择再加入选择列表
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
- 二叉树中和为某一值的路径
返回所有路径
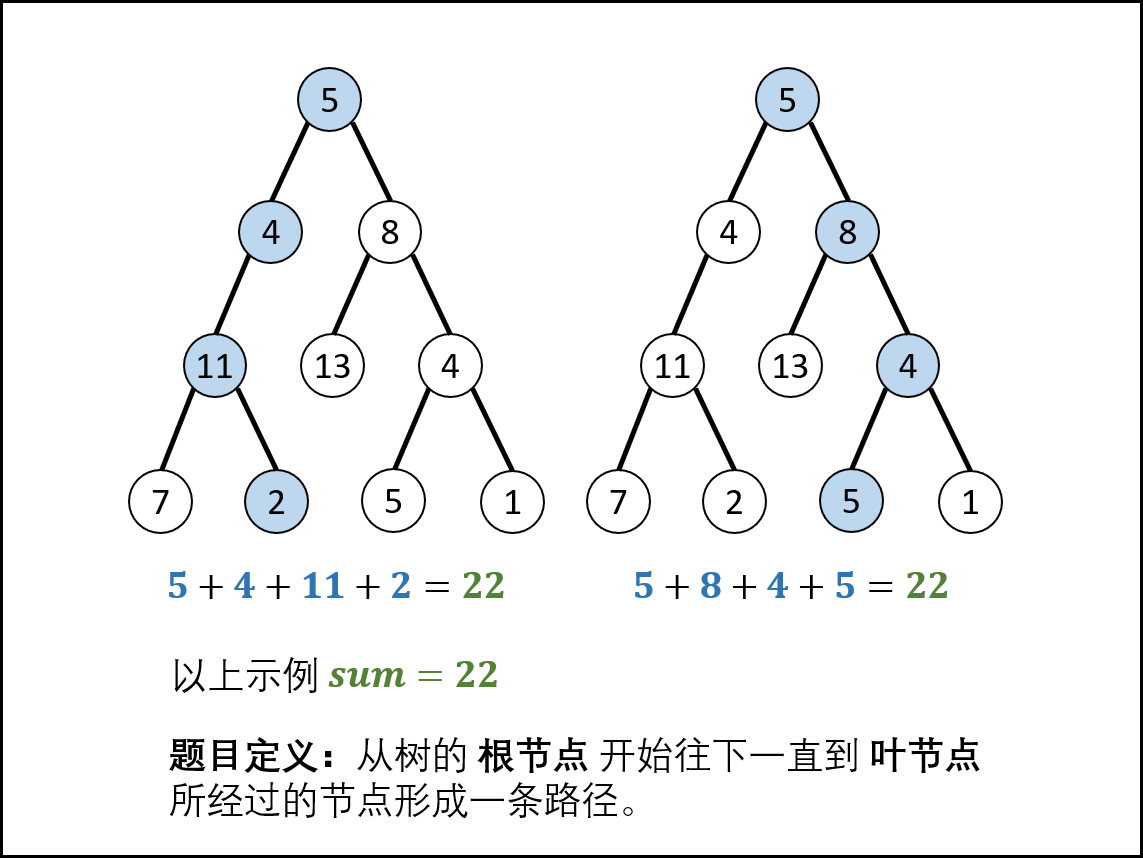
class Solution {
LinkedList<List<Integer>> res = new LinkedList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> pathSum(TreeNode root, int sum) {
recur(root, sum);
return res;
}
void recur(TreeNode root, int tar) {
if(root == null) return;
path.add(root.val);
tar -= root.val;
if(tar == 0 && root.left == null && root.right == null)
res.add(new LinkedList(path));
recur(root.left, tar);
recur(root.right, tar);
path.removeLast();
}
}
- 全排列问题

List<List<Integer>> res = new LinkedList<>();
/* 主函数,输入一组不重复的数字,返回它们的全排列 */
List<List<Integer>> permute(int[] nums) {
// 记录「路径」
LinkedList<Integer> track = new LinkedList<>();
backtrack(nums, track);
return res;
}
// 路径:记录在 track 中
// 选择列表:nums 中不存在于 track 的那些元素
// 结束条件:nums 中的元素全都在 track 中出现
void backtrack(int[] nums, LinkedList<Integer> track) {
// 触发结束条件
if (track.size() == nums.length) {
res.add(new LinkedList(track));
return;
}
for (int i = 0; i < nums.length; i++) {
// 排除不合法的选择
if (track.contains(nums[i]))
continue;
// 做选择
track.add(nums[i]);
// 进入下一层决策树
backtrack(nums, track);
// 取消选择
track.removeLast();
}
}
- 填充颜色
编写函数,实现许多图片编辑软件都支持的「颜色填充」功能。
待填充的图像用二维数组 image 表示,元素为初始颜色值。初始坐标点的横坐标为 sr 纵坐标为 sc。需要填充的新颜色为 newColor 。
「周围区域」是指颜色相同且在上、下、左、右四个方向上存在相连情况的若干元素。
请用新颜色填充初始坐标点的周围区域,并返回填充后的图像。
输入:
image = [[1,1,1],
[1,1,0],
[1,0,1]]
sr = 1, sc = 1, newColor = 2
输出:[
[2,2,2],
[2,2,0],
[2,0,1]]
解释:
初始坐标点位于图像的正中间,坐标 (sr,sc)=(1,1) 。
初始坐标点周围区域上所有符合条件的像素点的颜色都被更改成 2 。
注意,右下角的像素没有更改为 2 ,因为它不属于初始坐标点的周围区域。
DFS
class Solution {
public int[][] floodFill(int[][] image, int sr, int sc, int newColor) {
int oldColor = image[sr][sc];
dfs(image, sr, sc, newColor, oldColor);
return image;
}
private void dfs(int[][] image, int sr, int sc, int newColor, int oldColor){
if (sr < 0 || sc < 0 || sr >= image.length || sc >= image[0].length) {
return;
}
if (image[sr][sc] == oldColor && image[sr][sc] != newColor) {
image[sr][sc] = newColor;
dfs(image, sr + 1, sc, newColor, oldColor);
dfs(image, sr - 1, sc, newColor, oldColor);
dfs(image, sr, sc + 1, newColor, oldColor);
dfs(image, sr, sc - 1, newColor, oldColor);
}
}
}
- 二叉树所有路径
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
输入:
1
/
2 3
5
输出: ["1->2->5", "1->3"]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3
DFS
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> paths = new ArrayList<String>();
constructPaths(root, "", paths);
return paths;
}
public void constructPaths(TreeNode root, String path, List<String> paths) {
if (root != null) {
StringBuffer pathSB = new StringBuffer(path);
pathSB.append(Integer.toString(root.val));
if (root.left == null && root.right == null) { // 当前节点是叶子节点
paths.add(pathSB.toString()); // 把路径加入到答案中
return;
} else {
pathSB.append("->"); // 当前节点不是叶子节点,继续递归遍历
constructPaths(root.left, pathSB.toString(), paths);
constructPaths(root.right, pathSB.toString(), paths);
}
}
}
}
- 找树左下角的值
给定一个二叉树,在树的最后一行找到最左边的值。
示例 1:
输入:
2
/ \
1 3
输出:
1
示例 2:
输入:
1
/ \
2 3
/ / \
4 5 6
/
7
输出:
7
深度优先遍历DFS:记录深度最大的第一个节点
class Solution {
int[] result = new int[]{0,-1};
public int findBottomLeftValue(TreeNode root) {
dfs(root,0);
return result[0];
}
public void dfs(TreeNode root,int depth){
if(root==null) return ;
if(depth>result[1]){
result[0] = root.val;
result[1] = depth;
}
dfs(root.left,depth+1);
dfs(root.right,depth+1);
}
}
广度优先遍历BFS:按照从右往左的层序遍历,最后一个就是结果
class Solution {
public int findBottomLeftValue(TreeNode root) {
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while(!q.isEmpty()){
root = q.poll();
if(root.right!=null)
q.offer(root.right);
if(root.left!=null)
q.offer(root.left);
}
return root.val;
}
}
- 钥匙和房间
有 N 个房间,开始时你位于 0 号房间。每个房间有不同的号码:0,1,2,...,N-1,并且房间里可能有一些钥匙能使你进入下一个房间。
在形式上,对于每个房间 i 都有一个钥匙列表 rooms[i],每个钥匙 rooms[i][j] 由 [0,1,...,N-1] 中的一个整数表示,其中 N = rooms.length。 钥匙 rooms[i][j] = v 可以打开编号为 v 的房间。
最初,除 0 号房间外的其余所有房间都被锁住。
你可以自由地在房间之间来回走动。
如果能进入每个房间返回 true,否则返回 false。
示例 1:
输入: [[1],[2],[3],[]]
输出: true
解释:
我们从 0 号房间开始,拿到钥匙 1。
之后我们去 1 号房间,拿到钥匙 2。
然后我们去 2 号房间,拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间,我们返回 true。
示例 2:
输入:[[1,3],[3,0,1],[2],[0]]
输出:false
解释:我们不能进入 2 号房间。
DFS
我们可以使用深度优先搜索的方式遍历整张图,统计可以到达的节点个数,并利用数组 vis\textitvis 标记当前节点是否访问过,以防止重复访问。
class Solution {
boolean[] vis;
int num;
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
int n = rooms.size();
num = 0;
vis = new boolean[n];
dfs(rooms, 0);
return num == n;
}
public void dfs(List<List<Integer>> rooms, int x) {
vis[x] = true;
num++;
for (int it : rooms.get(x)) {
if (!vis[it]) {
dfs(rooms, it);
}
}
}
}
BFS
我们也可以使用广度优先搜索的方式遍历整张图,统计可以到达的节点个数,并利用数组 vis\textitvis 标记当前节点是否访问过,以防止重复访问。
class Solution {
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
int n = rooms.size(), num = 0;
boolean[] vis = new boolean[n];
Queue<Integer> que = new LinkedList<Integer>();
vis[0] = true;
que.offer(0);
while (!que.isEmpty()) {
int x = que.poll();
num++;
for (int it : rooms.get(x)) {
if (!vis[it]) {
vis[it] = true;
que.offer(it);
}
}
}
return num == n;
}
}
- 层数最深叶子节点的和
给你一棵二叉树,请你返回层数最深的叶子节点的和。
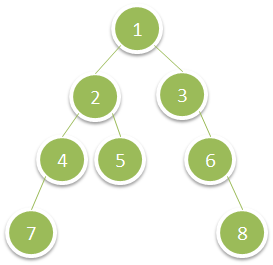
示例:
输入:root = [1,2,3,4,5,null,6,7,null,null,null,null,8]
输出:15
DFS
class Solution {
int maxDepth = -1;
int sum = 0;
public int deepestLeavesSum(TreeNode root) {
return dfs(root, 0);
}
private int dfs(TreeNode root, int depth) {
if (root == null) {
return 0;
}
if (maxDepth < depth) {
maxDepth = depth;
sum = root.val;
} else if (depth == maxDepth) {
sum += root.val;
}
if (root.left != null) {
dfs(root.left, depth + 1);
}
if (root.right != null) {
dfs(root.right, depth + 1);
}
return sum;
}
}
Java版本的层序遍历,只需要每层求和并判断是不是最后一层即可
class Solution {
public int deepestLeavesSum(TreeNode root) {
if (root == null) {
return 0;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int sum = 0;
int count = queue.size();
for (int i = 0; i < count; i++) {
root = queue.poll();
sum += root.val;
if (root.left != null) {
queue.offer(root.left);
}
if (root.right != null) {
queue.offer(root.right);
}
}
if (queue.isEmpty()) {
return sum;
}
}
throw null;
}
}
第二章 BFS(广度优先搜索)
算法框架
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
Queue<Node> q; // 核心数据结构
Set<Node> visited; // 避免走回头路
q.offer(start); // 将起点加入队列
visited.add(start);
int step = 0; // 记录扩散的步数
while (q not empty) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
/* 划重点:这里判断是否到达终点 */
if (cur is target)
return step;
/* 将 cur 的相邻节点加入队列 */
for (Node x : cur.adj())
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
/* 划重点:更新步数在这里 */
step++;
}
}
- 二叉树最小深度

int minDepth(TreeNode root) {
if (root == null) return 0;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
// root 本身就是一层,depth 初始化为 1
int depth = 1;
while (!q.isEmpty()) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
/* 判断是否到达终点 */
if (cur.left == null && cur.right == null)
return depth;
/* 将 cur 的相邻节点加入队列 */
if (cur.left != null)
q.offer(cur.left);
if (cur.right != null)
q.offer(cur.right);
}
/* 这里增加步数 */
depth++;
}
return depth;
}
- 二叉树最大深度
(1)BFS:层序遍历。一次处理一层,统计层数。
class Solution {
public int maxDepth(Node root) {
if(root == null) return 0;
int layer = 0;
Queue<Node> q = new LinkedList<>();
q.offer(root);
while(!q.isEmpty())
{
layer++;
int sz = q.size();
for(int i = 0; i < sz; i++)
{
Node cur = q.poll();
for(var subNode : cur.children)
if(subNode != null)
q.offer(subNode);
}
}
return layer;
}
}
(2)DFS:一棵树的最大深度就是子树最大深度的最大值加一。
class Solution {
public int maxDepth(Node root) {
if(root == null) return 0;
int subMax = 0;
for(var subNode : root.children)
{
int temp = maxDepth(subNode);
subMax = Math.max(subMax, temp);
}
return subMax + 1;
}
}
- 二叉树层序遍历**
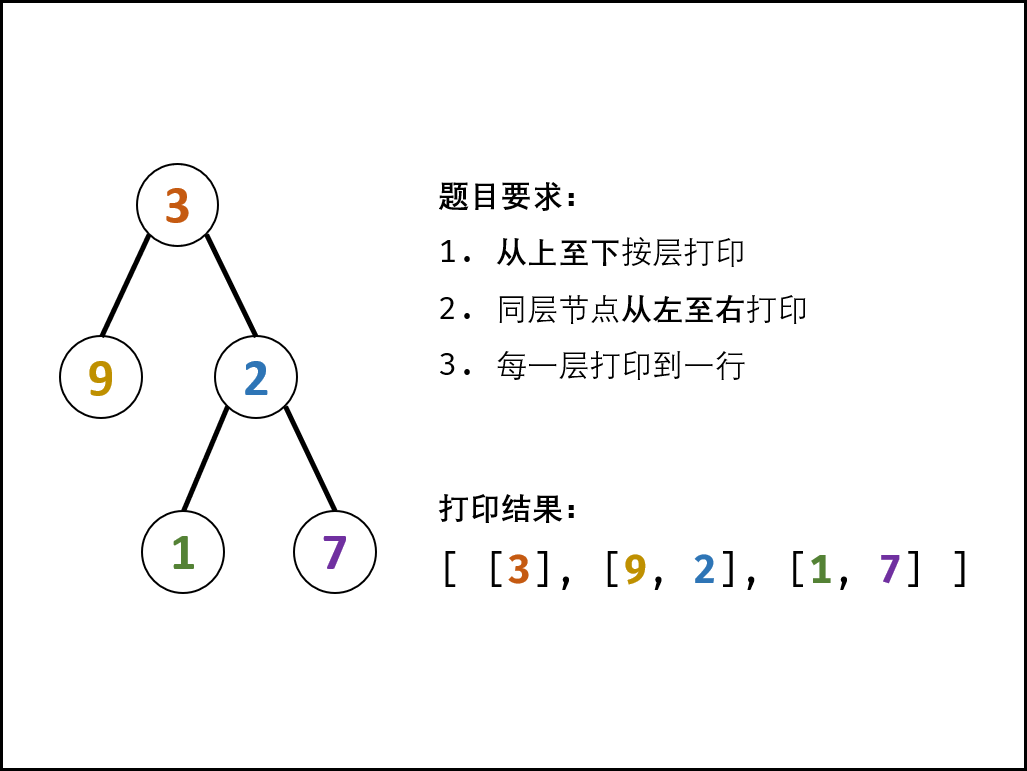
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
if(root != null) queue.add(root);
while(!queue.isEmpty()) {
List<Integer> tmp = new ArrayList<>();
for(int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
tmp.add(node.val);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
res.add(tmp);
}
return res;
}
}
- 课程表
现在你总共有 n 门课需要选,记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件,返回你为了学完所有课程所安排的学习顺序。
可能会有多个正确的顺序,你只要返回一种就可以了。如果不可能完成所有课程,返回一个空数组。
输入: 4, [[1,0],[2,0],[3,1],[3,2]]
输出: [0,1,2,3] or [0,2,1,3]
解释: 总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
BFS 的总体思路:
- 建立入度表,入度为 0 的节点先入队
- 当队列不为空,节点出队,标记学完课程数量的变量加 1,并记录该课程
- 将课程的邻居入度减 1
- 若邻居课程入度为 0,加入队列
- 用一个变量记录学完的课程数量,一个数组记录最终结果,简洁好理解。
DFS 的总体思路:
- 建立邻接矩阵
- DFS 访问每一个课程,若存在环直接返回
- status 保存课程的访问状态,同一个栈保存课程的访问序列。
// 方法 1 最简单的 BFS
public int[] findOrder(int numCourses, int[][] prerequisites) {
if (numCourses == 0) return new int[0];
int[] inDegrees = new int[numCourses];
// 建立入度表
for (int[] p : prerequisites) { // 对于有先修课的课程,计算有几门先修课
inDegrees[p[0]]++;
}
// 入度为0的节点队列
Queue<Integer> queue = new LinkedList<>();
for (int i = 0; i < inDegrees.length; i++) {
if (inDegrees[i] == 0) queue.offer(i);
}
int count = 0; // 记录可以学完的课程数量
int[] res = new int[numCourses]; // 可以学完的课程
// 根据提供的先修课列表,删除入度为 0 的节点
while (!queue.isEmpty()){
int curr = queue.poll();
res[count++] = curr; // 将可以学完的课程加入结果当中
for (int[] p : prerequisites) {
if (p[1] == curr){
inDegrees[p[0]]--;
if (inDegrees[p[0]] == 0) queue.offer(p[0]);
}
}
}
if (count == numCourses) return res;
return new int[0];
}
// 方法 2:邻接矩阵 + DFS 由于用的数组,每次都要遍历,效率比较低
public int[] findOrder(int numCourses, int[][] prerequisites) {
if (numCourses == 0) return new int[0];
// 建立邻接矩阵
int[][] graph = new int[numCourses][numCourses];
for (int[] p : prerequisites) {
graph[p[1]][p[0]] = 1;
}
// 记录访问状态的数组,访问过了标记 -1,正在访问标记 1,还未访问标记 0
int[] status = new int[numCourses];
Stack<Integer> stack = new Stack<>(); // 用栈保存访问序列
for (int i = 0; i < numCourses; i++) {
if (!dfs(graph, status, i, stack)) return new int[0]; // 只要存在环就返回
}
int[] res = new int[numCourses];
for (int i = 0; i < numCourses; i++) {
res[i] = stack.pop();
}
return res;
}
private boolean dfs(int[][] graph, int[] status, int i, Stack<Integer> stack) {
if (status[i] == 1) return false; // 当前节点在此次 dfs 中正在访问,说明存在环
if (status[i] == -1) return true;
status[i] = 1;
for (int j = 0; j < graph.length; j++) {
// dfs 访问当前课程的后续课程,看是否存在环
if (graph[i][j] == 1 && !dfs(graph, status, j, stack)) return false;
}
status[i] = -1; // 标记为已访问
stack.push(i);
return true;
}
5.岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
输入:
[
['1','1','1','1','0'],
['1','1','0','1','0'],
['1','1','0','0','0'],
['0','0','0','0','0']
]输出: 1
BFS
class Solution {
public int numIslands(char[][] grid) {
int count = 0;
for(int i = 0; i < grid.length; i++) {
for(int j = 0; j < grid[0].length; j++) {
if(grid[i][j] == '1'){
bfs(grid, i, j);
count++;
}
}
}
return count;
}
private void bfs(char[][] grid, int i, int j){
Queue<int[]> list = new LinkedList<>();
list.add(new int[] { i, j });
while(!list.isEmpty()){
int[] cur = list.remove();
i = cur[0]; j = cur[1];
if(0 <= i && i < grid.length && 0 <= j && j < grid[0].length && grid[i][j] == '1') {
grid[i][j] = '0'; //注意这里
list.add(new int[] { i + 1, j });
list.add(new int[] { i - 1, j });
list.add(new int[] { i, j + 1 });
list.add(new int[] { i, j - 1 });
}
}
}
}
- 01矩阵
给定一个由 0 和 1 组成的矩阵,找出每个元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
输入:
0 0 0
0 1 0
1 1 1输出:
0 0 0
0 1 0
1 2 1
BFS
public int[][] updateMatrix(int[][] matrix) {
if (matrix == null || matrix.length == 0) return null;
int m = matrix.length, n = matrix[0].length;
int[][] res = new int[m][n];//结果集
boolean[][] visited = new boolean[m][n];//记录已经计算过的位置
Queue<int[]> queue = new LinkedList<>();//广搜队列
//遍历,将等于0的位置计入结果集并入队
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == 0) {
res[i][j] = 0;
visited[i][j] = true;
queue.offer(new int[]{i, j});
}
}
}
//四个方向广搜
int[][] direction = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};//上下左右
while (!queue.isEmpty()) {
int[] poll = queue.poll();
int i = poll[0], j = poll[1];
//四个方向上找 1
for (int k = 0; k < 4; k++) {
int di = i + direction[k][0], dj = j + direction[k][1];
//没有计算过的地方一定是 1
if (di >= 0 && di < m && dj >= 0 && dj < n && !visited[di][dj]) {
res[di][dj] = res[i][j] + 1;
visited[di][dj] = true;
queue.offer(new int[]{di, dj});
}
}
}
return res;
}
- 在每个树行中找到最大值
需要在二叉树的每一行中找到最大的值。
示例:
输入:
1
/ \
3 2
/ \ \
5 3 9
BFS
public List<Integer> largestValues(TreeNode root) {
//LinkedList实现队列
Queue<TreeNode> queue = new LinkedList<>();
List<Integer> values = new ArrayList<>();
if (root != null)
queue.add(root);//入队
while (!queue.isEmpty()) {
int max = Integer.MIN_VALUE;
int levelSize = queue.size();//每一层的数量
for (int i = 0; i < levelSize; i++) {
TreeNode node = queue.poll();//出队
max = Math.max(max, node.val);//记录每层的最大值
if (node.left != null)
queue.add(node.left);
if (node.right != null)
queue.add(node.right);
}
values.add(max);
}
return values;
}
第三章 动态规划(DP)
算法框架
# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 求最值(选择1,选择2...)
- 礼物的最大价值
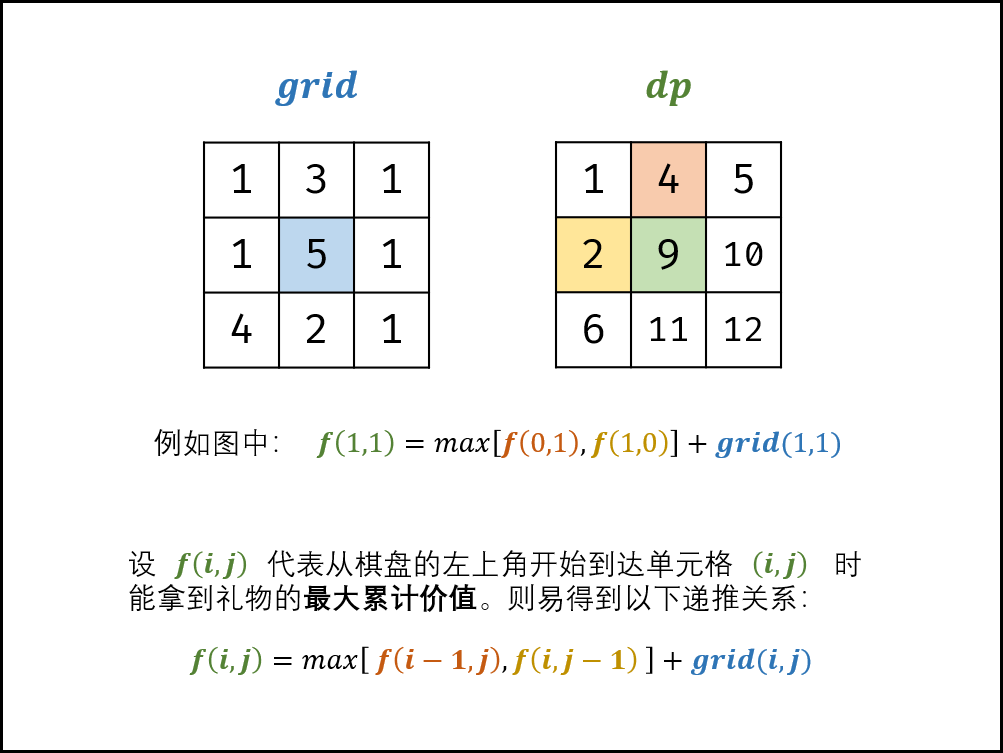
class Solution {
public int maxValue(int[][] grid) {
int m = grid.length, n = grid[0].length;
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
if(i == 0 && j == 0) continue;
if(i == 0) grid[i][j] += grid[i][j - 1] ;
else if(j == 0) grid[i][j] += grid[i - 1][j];
else grid[i][j] += Math.max(grid[i][j - 1], grid[i - 1][j]);
}
}
return grid[m - 1][n - 1];
}
}
- n个骰子的点数
class Solution {
public double[] twoSum(int n) {
int[][] dp = new int[n + 1][6 * n + 1];//dp[骰子个数][所有可能的值]
for (int i = 1; i <= 6; i++) {
dp[1][i] = 1; //表示一个骰子掷出i点的次数为1
}
for (int i = 2; i <= n; i++) {//i代表当前骰子的个数
for (int j = i; j <= 6 * n; j++) {//j代表当前值的和 表示可能会出现的点数之和
for (int k = 1; k <= 6&&k<=j; k++) {//k代表当前筛子的值 当总数还没有j大时,就不存在这种情况
//状态转移方程: i个骰子和为j += i-1个骰子和为j-k + 第i个骰子值为k
dp[i][j] += dp[i-1][j - k];
}
}
}
final double totalNum = Math.pow(6, n);//总次数
double[] ans = new double[5*n+1];
for(int i=n;i<=6*n;i++){
ans[i-n]=((double)dp[n][i])/totalNum;
}
return ans;
}
}
//考虑用动归,数组 dp[i] [j]表示用 i 个骰子扔出和为 j 的可能数,因为第i个骰子可能扔出 1-6 的点数,则
//dp[i][j]=dp[i-1][j-1]+dp[i-1][j-2]+dp[i-1][j-3]+dp[i-1][j-4]+dp[i-1][j-5]+dp[i-1][j-6]
- 0-1背包问题
| w | v | i\j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 6 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| 2 | 3 | 1 | 0 | 0 | 6 | 6 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| 6 | 5 | 2 | 0 | 0 | 6 | 6 | 9 | 9 | 9 | 9 | 11 | 11 | 14 |
| 5 | 4 | 3 | 0 | 0 | 6 | 6 | 9 | 9 | 9 | 10 | 11 | 13 | 14 |
| 4 | 6 | 4 | 0 | 0 | 6 | 6 | 9 | 9 | 12 | 12 | 15 | 15 | 15 |
int knapsack(int W, int N, vector<int>& wt, vector<int>& val) {
// vector 全填入 0,base case 已初始化
vector<vector<int>> dp(N + 1, vector<int>(W + 1, 0));
for (int i = 1; i <= N; i++) {
for (int w = 1; w <= W; w++) {
if (w - wt[i-1] < 0) {
// 当前背包容量装不下,只能选择不装入背包
dp[i][w] = dp[i - 1][w];
} else {
// 装入或者不装入背包,择优
dp[i][w] = max(dp[i - 1][w - wt[i-1]] + val[i-1],
dp[i - 1][w]);
}
}
}
return dp[N][W];
}
- 最长上升子序列
叠罗汉类似问题
输入:height = [65,70,56,75,60,68] weight = [100,150,90,190,95,110]
输出:6
解释:从上往下数,叠罗汉最多能叠 6 层:(56,90), (60,95), (65,100), (68,110), (70,150), (75,190)(将一个身高固定,再求最长上升子序列)
解题思路
1.将height数组先排序。
2.根据题意,height数组排序之后,对weight数组中,height相同的人的weight按降序排序。
3.对此时的weight数组求最长递增子序列的长度,即是答案。

// Dynamic programming.
class Solution {
public int lengthOfLIS(int[] nums) {
if(nums.length == 0) return 0;
int[] dp = new int[nums.length];
int res = 0;
Arrays.fill(dp, 1);
for(int i = 0; i < nums.length; i++) {
for(int j = 0; j < i; j++) {
if(nums[j] < nums[i]) dp[i] = Math.max(dp[i], dp[j] + 1);
}
res = Math.max(res, dp[i]);
}
return res;
}
}
- 字符串拆分
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明:
拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
public class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
Set<String> wordDictSet = new HashSet(wordDict);
boolean[] dp = new boolean[s.length() + 1];
dp[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i; j++) {
if (dp[j] && wordDictSet.contains(s.substring(j, i))) {
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}
}
- 最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。若这两个字符串没有公共子序列,则返回 0。
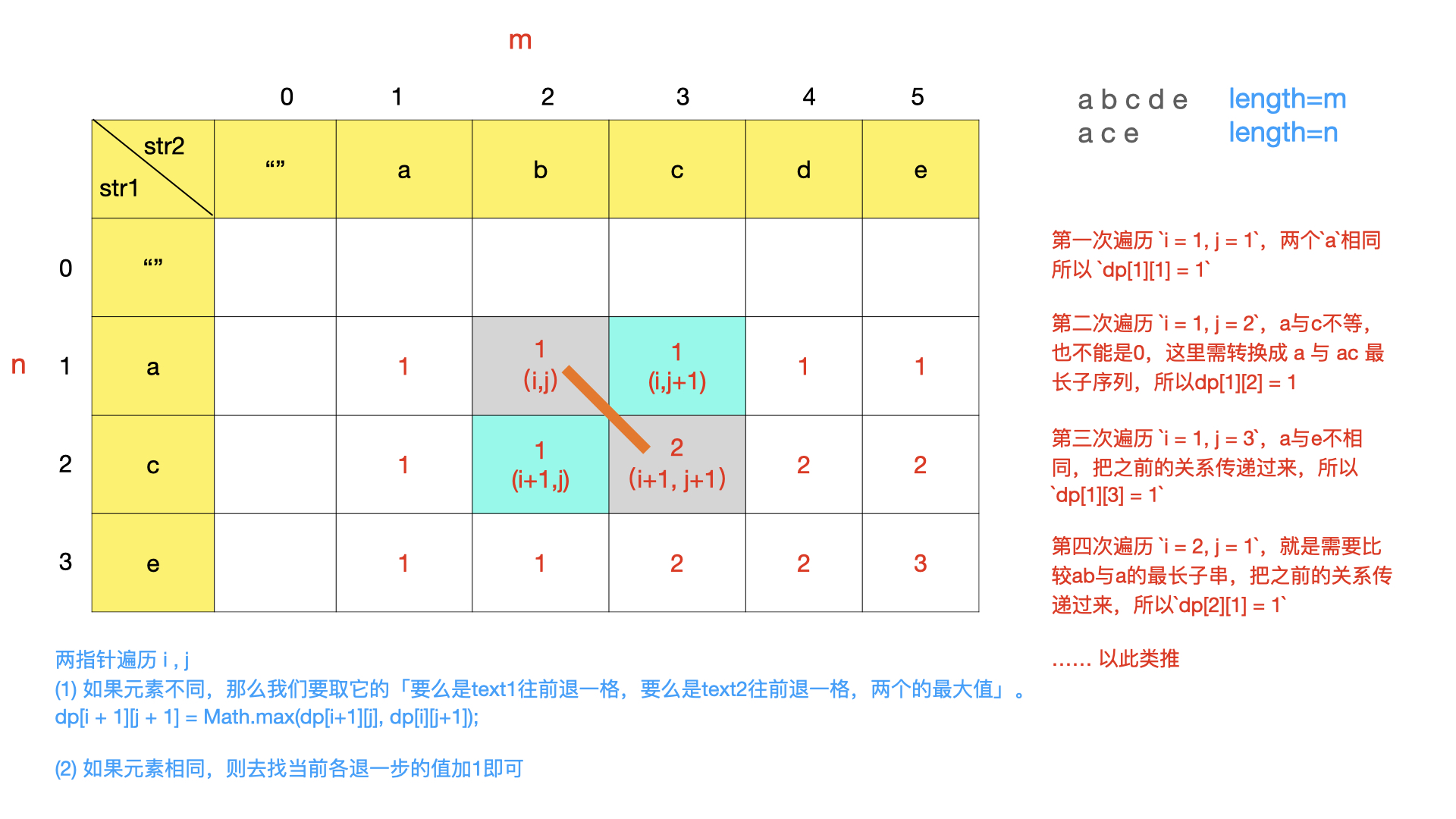
**输入:**text1 = "abcde", text2 = "ace"
**输出:**3
**解释:**最长公共子序列是 "ace",它的长度为 3。
// java
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int m = text1.length(), n = text2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 获取两个串字符
char c1 = text1.charAt(i), c2 = text2.charAt(j);
if (c1 == c2) {
// 去找它们前面各退一格的值加1即可
dp[i + 1][j + 1] = dp[i][j] + 1;
} else {
//要么是text1往前退一格,要么是text2往前退一格,两个的最大值
dp[i + 1][j + 1] = Math.max(dp[i + 1][j], dp[i][j + 1]);
}
}
}
return dp[m][n];
}
}
- 分割等和子集
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
注意:
每个数组中的元素不会超过 100
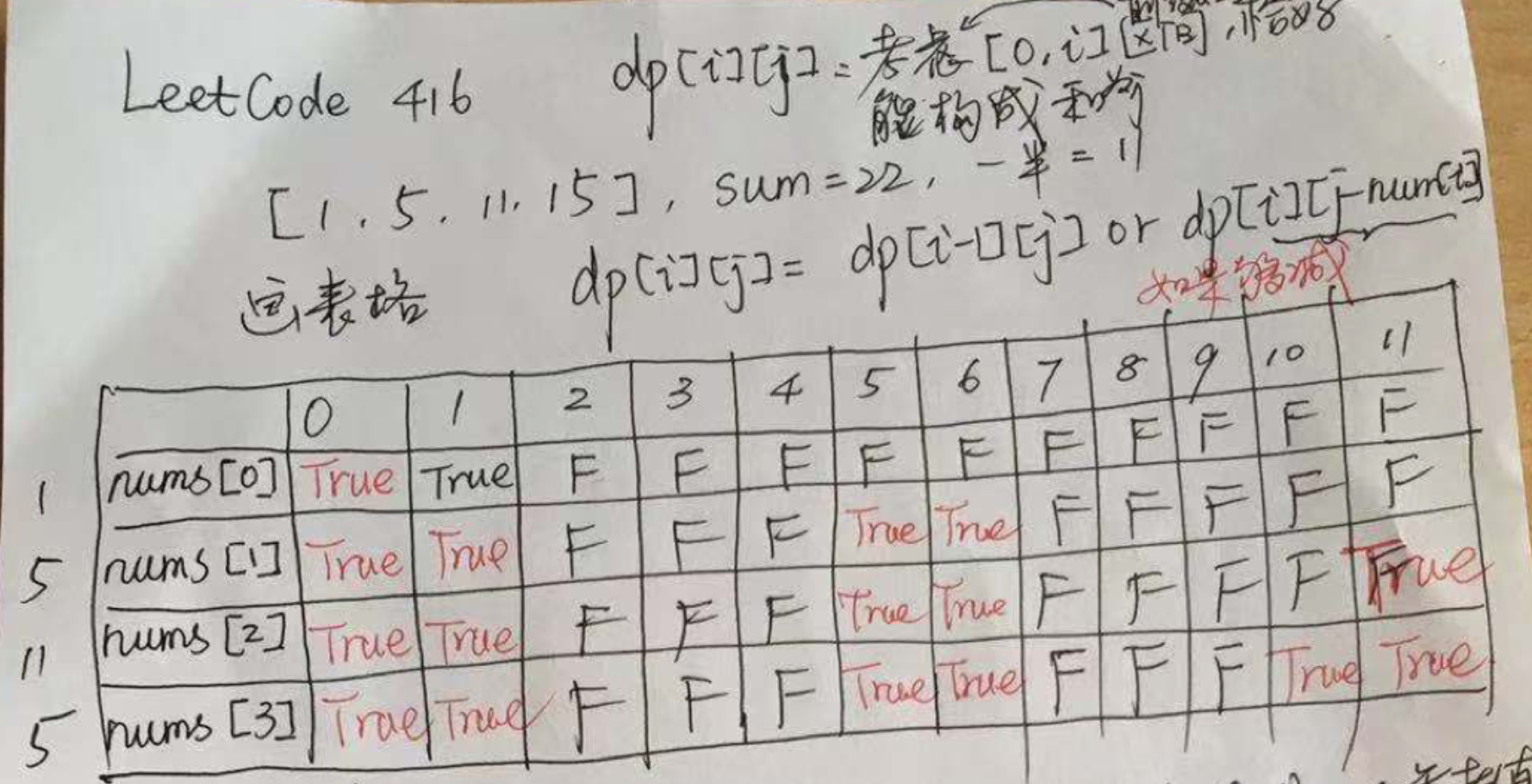
数组的大小不会超过 200输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].
public class Solution {
public boolean canPartition(int[] nums) {
int len = nums.length;
if (len == 0) {
return false;
}
int sum = 0;
for (int num : nums) {
sum += num;
}
// 特判:如果是奇数,就不符合要求
if ((sum & 1) == 1) {
return false;
}
int target = sum / 2;
// 创建二维状态数组,行:物品索引,列:容量(包括 0)
boolean[][] dp = new boolean[len][target + 1];
// 先填表格第 0 行,第 1 个数只能让容积为它自己的背包恰好装满
if (nums[0] <= target) {
dp[0][nums[0]] = true;
}
// 再填表格后面几行
for (int i = 1; i < len; i++) {
for (int j = 0; j <= target; j++) {
// 直接从上一行先把结果抄下来,然后再修正
dp[i][j] = dp[i - 1][j];
if (nums[i] == j) {
dp[i][j] = true;
continue;
}
if (nums[i] < j) {
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
}
}
}
return dp[len - 1][target];
}
}
//第二种解法
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0;
//计算数组的和sum,如果sum为奇数,那肯定不能分成两部分,直接返回false
for(int i = 0; i<nums.length; i++)
sum += nums[i];
if(sum % 2 != 0)
return false;
sum = sum/2;
//初始化base case :dp[...][0] = true,相当于当载重量为0的时候,肯定什么东西也不用放,背包肯定默认是满的,因为载重量为0嘛,所以是true;dp[0][...] = false,相当于在任一载重量时,什么东西都不放,那肯定背包没有满,所以是false
boolean[][] dp = new boolean[nums.length+1][sum+1];
for(int i = 0; i<nums.length+1; i++)
dp[i][0] = true;
//这里可以省略,因为java中boolean量默认是false,这里没有注释掉是因为想把逻辑表达清楚。
for(int i = 0; i<sum+1; i++)
dp[0][i] = false;
for(int i = 1; i<=nums.length; i++){
for(int j = 1; j<=sum; j++){
//如果当前的背包容量比要放的数量都小,那就没法放,只能继承之前的状态
if(j < nums[i-1]) dp[i][j] = dp[i-1][j];
else{
//放入或者不放入,不管哪种状态,只要能放满就可以
dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i-1]];
}
}
}
return dp[nums.length][sum];
}
}
第四章 滑动窗口
-
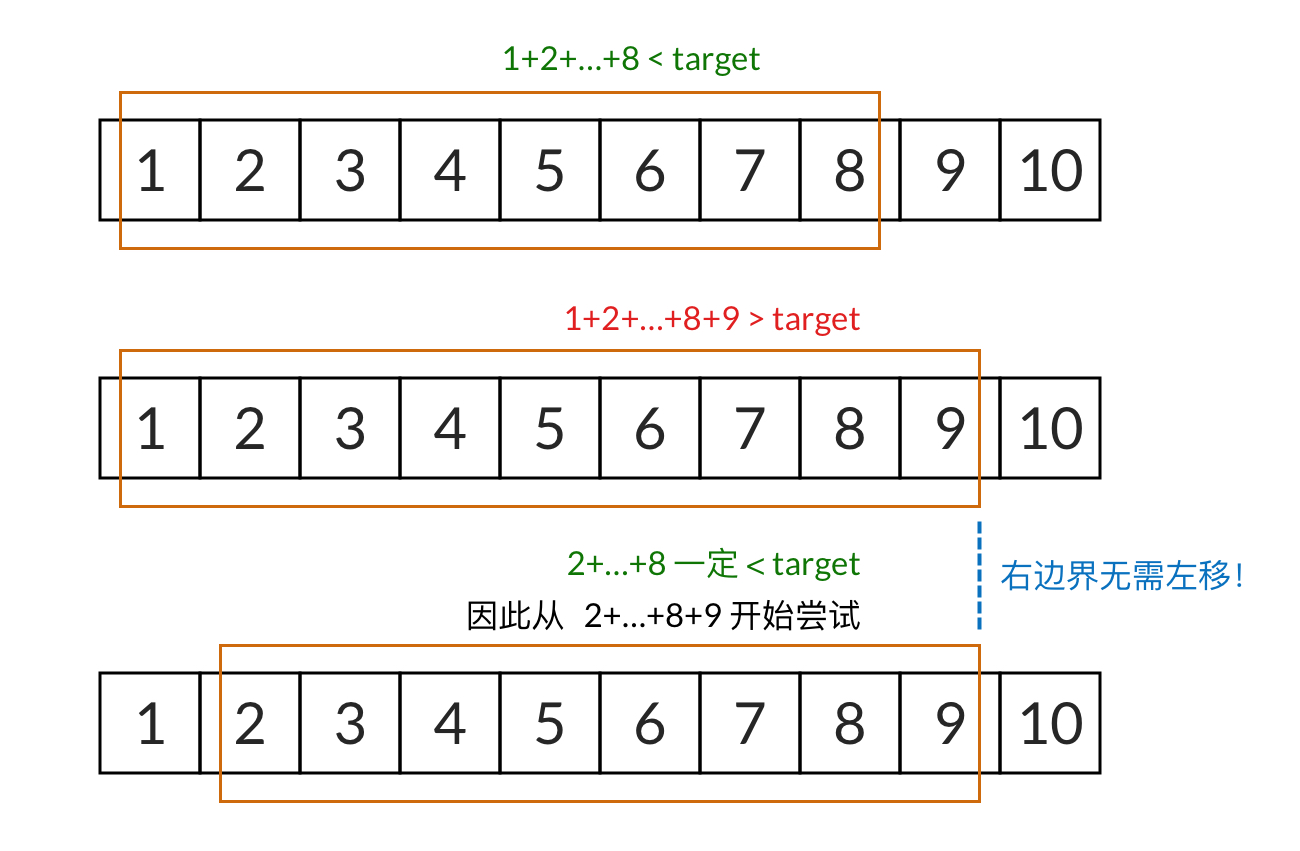
输入一个正整数
target,输出所有和为target的连续正整数序列(至少含有两个数)。示例 1:
输入:target = 9 输出:[[2,3,4],[4,5]]
public int[][] findContinuousSequence(int target) {
int i = 1; // 滑动窗口的左边界
int j = 1; // 滑动窗口的右边界
int sum = 0; // 滑动窗口中数字的和
List<int[]> res = new ArrayList<>();
while (i <= target / 2) {
if (sum < target) {
// 右边界向右移动
sum += j;
j++;
} else if (sum > target) {
// 左边界向右移动
sum -= i;
i++;
} else {
// 记录结果
int[] arr = new int[j-i];
for (int k = i; k < j; k++) {
arr[k-i] = k;
}
res.add(arr);
// 左边界向右移动
sum -= i;
i++;
}
}
return res.toArray(new int[res.size()][]);
}
第五章 双指针
- 区间列表的交集
给定两个由一些 闭区间 组成的列表,每个区间列表都是成对不相交的,并且已经排序。
返回这两个区间列表的交集。
(形式上,闭区间 [a, b](其中 a <= b)表示实数 x 的集合,而 a <= x <= b。两个闭区间的交集是一组实数,要么为空集,要么为闭区间。例如,[1, 3] 和 [2, 4] 的交集为 [2, 3]。)
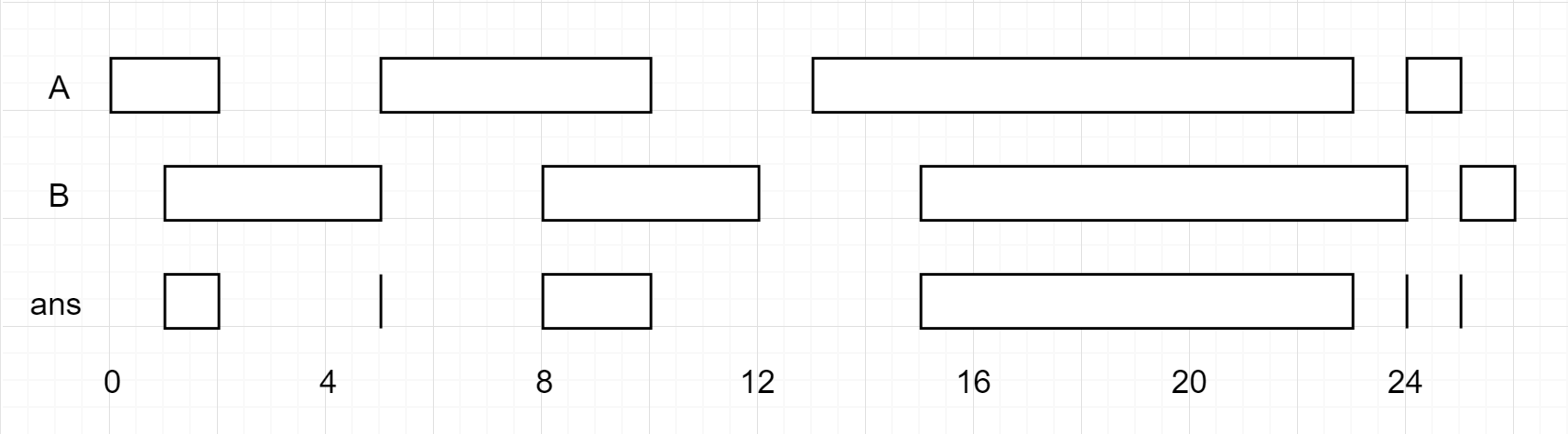
输入:A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
输出:[[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
class Solution {
public int[][] intervalIntersection(int[][] A, int[][] B) {
List<int[]> ans = new ArrayList();
int i = 0, j = 0;
while (i < A.length && j < B.length) {
// Let's check if A[i] intersects B[j].
// lo - the startpoint of the intersection
// hi - the endpoint of the intersection
int lo = Math.max(A[i][0], B[j][0]);
int hi = Math.min(A[i][1], B[j][1]);
if (lo <= hi)
ans.add(new int[]{lo, hi});
// Remove the interval with the smallest endpoint
if (A[i][1] < B[j][1])
i++;
else
j++;
}
return ans.toArray(new int[ans.size()][]);
}
}
- 三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList<>();
for(int k = 0; k < nums.length - 2; k++){
if(nums[k] > 0) break;
if(k > 0 && nums[k] == nums[k - 1]) continue;
int i = k + 1, j = nums.length - 1;
while(i < j){
int sum = nums[k] + nums[i] + nums[j];
if(sum < 0){
while(i < j && nums[i] == nums[++i]);
} else if (sum > 0) {
while(i < j && nums[j] == nums[--j]);
} else {
res.add(new ArrayList<Integer>(Arrays.asList(nums[k], nums[i], nums[j])));
while(i < j && nums[i] == nums[++i]);
while(i < j && nums[j] == nums[--j]);
}
}
}
return res;
}
}
- 盛最多水的容器
给你 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。

示例:
输入:[1,8,6,2,5,4,8,3,7]
输出:49
public class Solution {
public int maxArea(int[] height) {
int l = 0, r = height.length - 1;
int ans = 0;
while (l < r) {
int area = Math.min(height[l], height[r]) * (r - l);
ans = Math.max(ans, area);
if (height[l] <= height[r]) {
++l;
}
else {
--r;
}
}
return ans;
}
}
