算法笔记 2023
排序算法
插入排序
其他基本基于插入排序
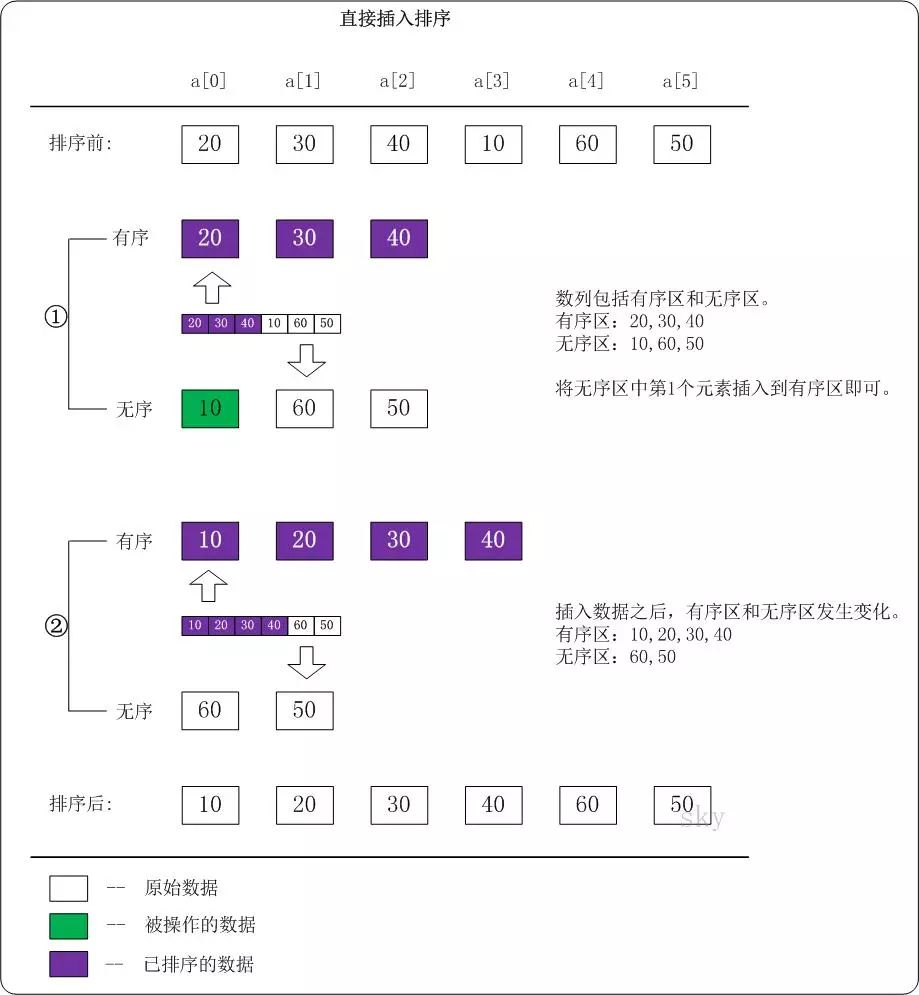
直接插入排序(Straight Insertion Sort)的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表。开始时有序表中只包含1个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,将它插入到有序表中的适当位置,使之成为新的有序表,重复n-1次可完成排序过程。
/**
* 插入排序
*
* @param sourceArray
* @return
* @throws Exception
*/
public int[] insertsort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
// 从下标为1的元素开始选择合适的位置插入,因为下标为0的只有一个元素,默认是有序的
for (int i = 1; i < arr.length; i++) {
// 记录要插入的数据
int tmp = arr[i];
// 从已经排序的序列最右边的开始比较,找到比其小的数
int j = i;
while (j > 0 && tmp < arr[j - 1]) {
arr[j] = arr[j - 1];
j--;
}
// 存在比其小的数,插入
if (j != i) {
arr[j] = tmp;
}
}
return arr;
}
归并排序
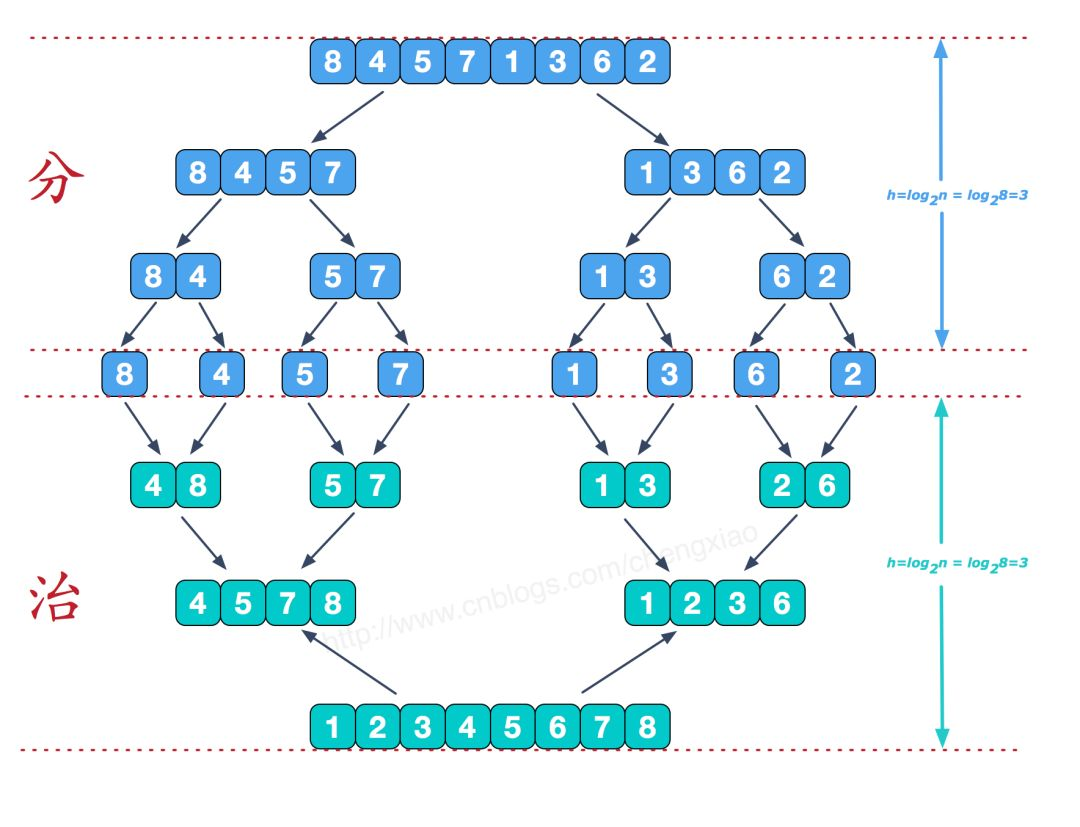
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
/**
* 归并排序
*
* @param sourceArray
* @return
* @throws Exception
*/
public int[] Mergesort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
if (arr.length < 2) {
return arr;
}
int middle = (int) Math.floor(arr.length / 2);
int[] left = Arrays.copyOfRange(arr, 0, middle);
int[] right = Arrays.copyOfRange(arr, middle, arr.length);
return merge(Mergesort(left), Mergesort(right));
}
protected int[] merge(int[] left, int[] right) {
int[] result = new int[left.length + right.length];
int i = 0;
while (left.length > 0 && right.length > 0) {
if (left[0] <= right[0]) {
result[i++] = left[0];
left = Arrays.copyOfRange(left, 1, left.length);
} else {
result[i++] = right[0];
right = Arrays.copyOfRange(right, 1, right.length);
}
}
while (left.length > 0) {
result[i++] = left[0];
left = Arrays.copyOfRange(left, 1, left.length);
}
while (right.length > 0) {
result[i++] = right[0];
right = Arrays.copyOfRange(right, 1, right.length);
}
return result;
}
快排
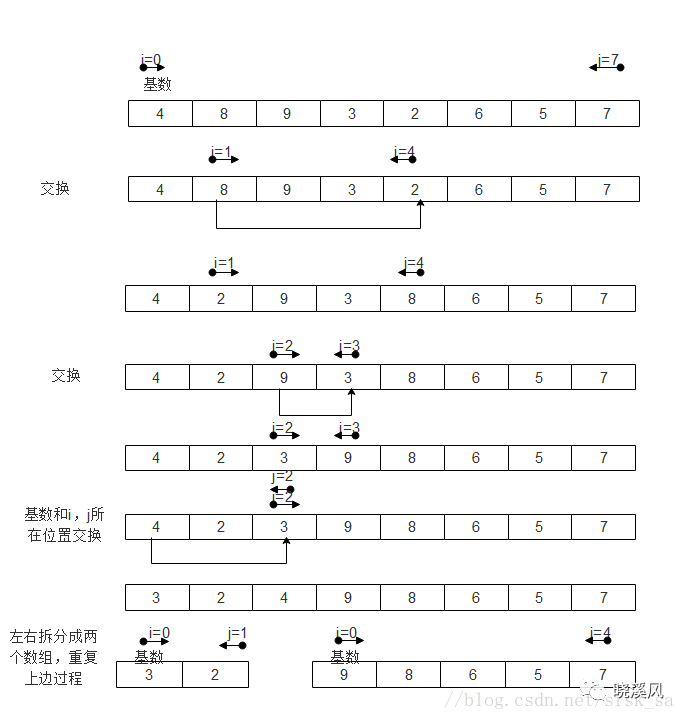
选择一个基准数,通过一趟排序将要排序的数据分割成独立的两部分;其中一部分的所有数据都比另外一部分的所有数据都要小。然后,再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。(左指针找第一个遇到的比基准值大的,右指针找第一个遇到的比基准值小的,若右指针下标此时小于左指针下标,则交换右指针元素有基准值,否则交换左右指针元素)
/**
* 快速排序 第二种算法
* @param R
* @param lo
* @param hi
* @return
*/
public int[] QuickSort1(int R[], int lo, int hi) {
int i = lo, j = hi;
int temp;
if (i < j) {
temp = R[i];
while (i != j) {
while (j > i && R[j] > temp) --j;
R[i] = R[j];
while (i < j && R[i] < temp) ++i;
R[j] = R[i];
}
R[i] = temp;
QuickSort1(R, lo, i - 1);
QuickSort1(R, i + 1, hi);
}
return R;
}
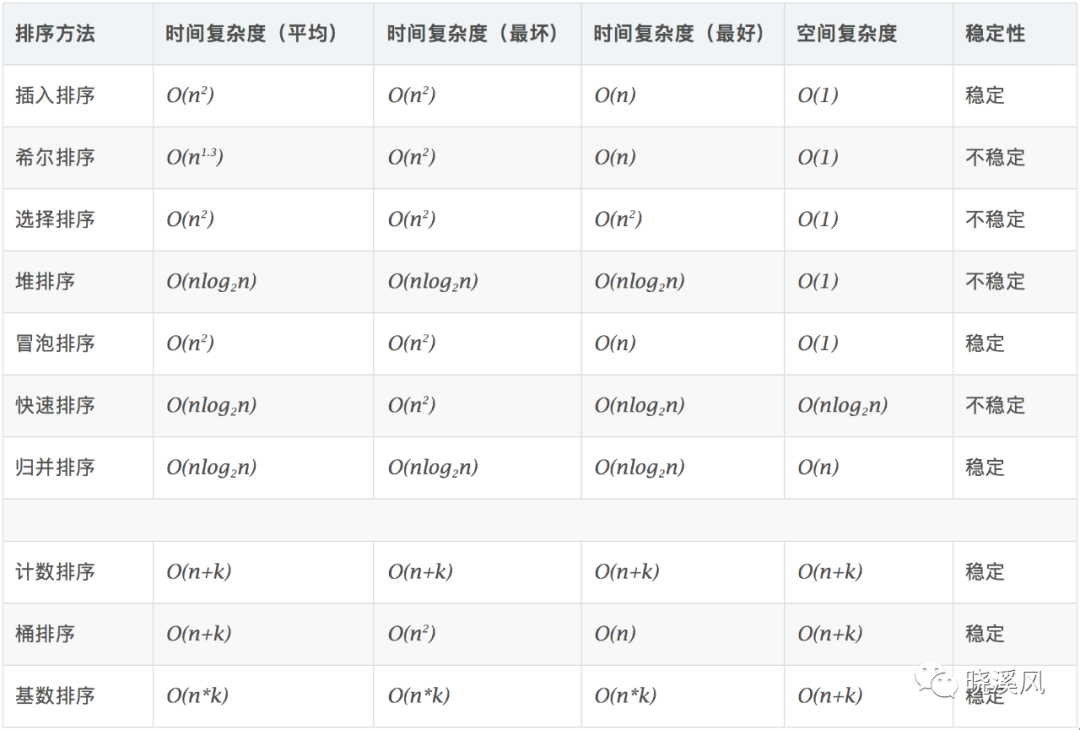
算法复杂度分析
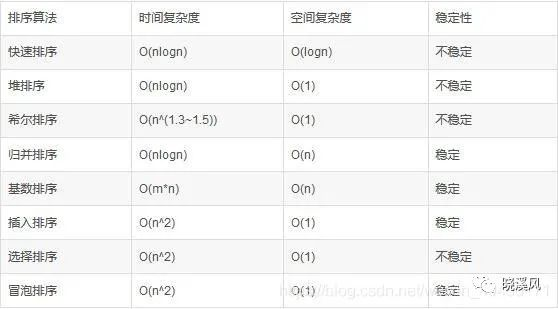
数组前缀和
案例1

代码实现
class NumArray {
// 前缀和数组
private int[] preSum;
/* 输⼊⼀个数组,构造前缀和 */
public NumArray(int[] nums) {
// preSum[0] = 0,便于计算累加和
preSum = new int[nums.length + 1];
// 计算 nums 的累加和
for (int i = 1; i < preSum.length; i++) {
preSum[i] = preSum[i - 1] + nums[i - 1];
}
}
/* 查询闭区间 [left, right] 的累加和 */
public int sumRange(int left, int right) {
return preSum[right + 1] - preSum[left];
}
}
差分数组
原理很简单,回想 diff 数组反推 nums 数组的过程,diff[i] += 3 意味着给 nums[i..] 所有的元素都加了 3,然后 diff[j+1] -= 3 ⼜意味着对于 nums[j+1..] 所有元素再减 3,那综合起来,是不是就是对
nums[i..j] 中的所有元素都加 3 了?
案例1

代码实现
// 差分数组⼯具类
class Difference {
// 差分数组
private int[] diff;
/* 输⼊⼀个初始数组,区间操作将在这个数组上进⾏ */
public Difference(int[] nums) {
assert nums.length > 0;
diff = new int[nums.length];
// 根据初始数组构造差分数组
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
/* 给闭区间 [i, j] 增加 val(可以是负数)*/
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}
/* 返回结果数组 */
public int[] result() {
int[] res = new int[diff.length];
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
}
调用上面的方法
int[] getModifiedArray(int length, int[][] updates) {
// nums 初始化为全 0
int[] nums = new int[length];
// 构造差分解法
Difference df = new Difference(nums);
for (int[] update : updates) {
int i = update[0];
int j = update[1];
int val = update[2];
df.increment(i, j, val);
}
return df.result();
}
双指针
(1) 合并两个有序链表

/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
ListNode p1=list1, p2=list2;
ListNode dummy = new ListNode(-1), p = dummy;
while(p1 != null && p2 != null){
if(p1.val > p2.val){
p.next = p2;
p2 = p2.next;
}else{
p.next = p1;
p1 = p1.next;
}
p = p.next;
}
if(p1 != null){
p.next = p1;
}
if(p2 != null){
p.next = p2;
}
return dummy.next;
}
}
(2) 合并 k 个有序链表

ListNode mergeKLists(ListNode[] lists) {
if (lists.length == 0) return null;
// 虚拟头结点
ListNode dummy = new ListNode(-1);
ListNode p = dummy;
// 优先级队列,最⼩堆
PriorityQueue<ListNode> pq = new PriorityQueue<>(
lists.length, (a, b)->(a.val - b.val));
// 将 k 个链表的头结点加⼊最⼩堆
for (ListNode head : lists) {
if (head != null)
pq.add(head);
}
while (!pq.isEmpty()) {
// 获取最⼩节点,接到结果链表中
ListNode node = pq.poll();
p.next = node;
if (node.next != null) {
pq.add(node.next);
}
// p 指针不断前进
p = p.next;
}
return dummy.next;
}
(3) 快慢指针

int removeDuplicates(int[] nums) {
if (nums.length == 0) {
return 0;
}
int slow = 0, fast = 0;
while (fast < nums.length) {
if (nums[fast] != nums[slow]) {
slow++;
// 维护 nums[0..slow] ⽆重复
nums[slow] = nums[fast];
}
fast++;
}
// 数组⻓度为索引 + 1
return slow + 1;
}
(4) 两数之和

类似二分查找算法
int[] twoSum(int[] nums, int target) {
// ⼀左⼀右两个指针相向⽽⾏
int left = 0, right = nums.length - 1;
while (left < right) {
int sum = nums[left] + nums[right];
if (sum == target) {
// 题⽬要求的索引是从 1 开始的
return new int[]{left + 1, right + 1};
} else if (sum < target) {
left++; // 让 sum ⼤⼀点
} else if (sum > target) {
right--; // 让 sum ⼩⼀点
}
}
return new int[]{-1, -1};
}
反转数组类似左右交换
void reverseString(char[] s) {
// ⼀左⼀右两个指针相向⽽⾏
int left = 0, right = s.length - 1;
while (left < right) {
// 交换 s[left] 和 s[right]
char temp = s[left];
s[left] = s[right];
s[right] = temp;
left++;
right--;
}
}
(5) 最长回文子串
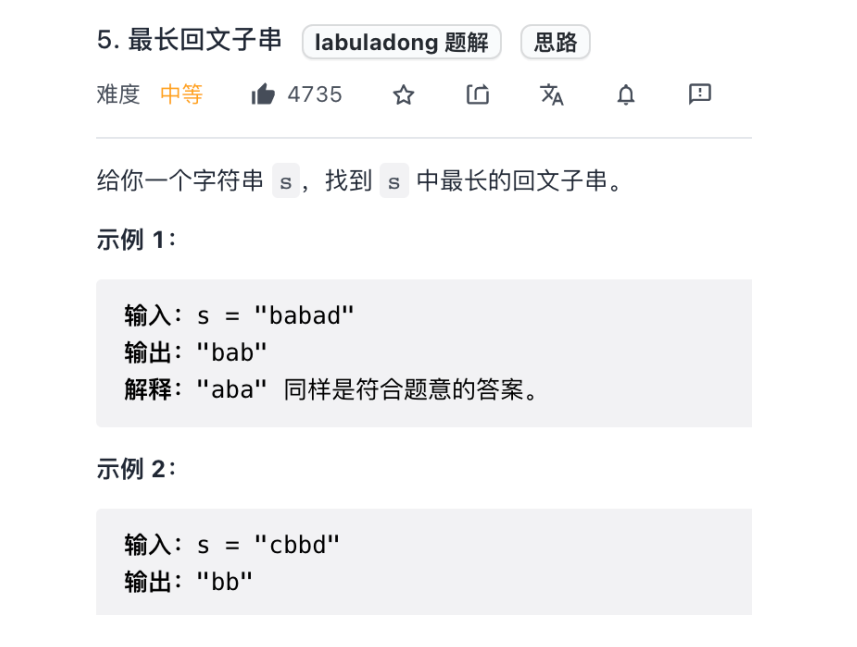
// 在 s 中寻找以 s[l] 和 s[r] 为中⼼的最⻓回⽂串
String palindrome(String s, int l, int r) {
// 防⽌索引越界
while (l >= 0 && r < s.length()
&& s.charAt(l) == s.charAt(r)) {
// 双指针,向两边展开
l--; r++;
}
// 返回以 s[l] 和 s[r] 为中⼼的最⻓回⽂串
return s.substring(l + 1, r);
}
String longestPalindrome(String s) {
String res = "";
for (int i = 0; i < s.length(); i++) {
// 以 s[i] 为中⼼的最⻓回⽂⼦串
String s1 = palindrome(s, i, i);
// 以 s[i] 和 s[i+1] 为中⼼的最⻓回⽂⼦串
String s2 = palindrome(s, i, i + 1);
// res = longest(res, s1, s2)
res = res.length() > s1.length() ? res : s1;
res = res.length() > s2.length() ? res : s2;
}
return res;
}
你应该能发现最⻓回⽂⼦串使⽤的左右指针和之前题⽬的左右指针有⼀些不同:之前的左右指针都是从两端向中间相向⽽⾏,⽽回⽂⼦串问题则是让左右指针从中⼼向两端扩展。不过这种情况也就回⽂串这类问题会遇到
滑动窗口
算法框架
/* 滑动窗口算法框架 */
void slidingWindow(String s) {
// 用合适的数据结构记录窗口中的数据
HashMap<Character, Integer> window = new HashMap<>();
int left = 0, right = 0;
while (right < s.length()) {
// c 是将移入窗口的字符
char c = s.charAt(right);
window.put(c, window.getOrDefault(c, 0) + 1);
// 增大窗口
right++;
// 进行窗口内数据的一系列更新
...
/*** debug 输出的位置 ***/
// 注意在最终的解法代码中不要 print
// 因为 IO 操作很耗时,可能导致超时
System.out.printf("window: [%d, %d)\n", left, right);
/********************/
// 判断左侧窗口是否要收缩
while (left < right && window needs shrink) {
// d 是将移出窗口的字符
char d = s.charAt(left);
window.put(d, window.get(d) - 1);
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
}
(1) 最小覆盖子串
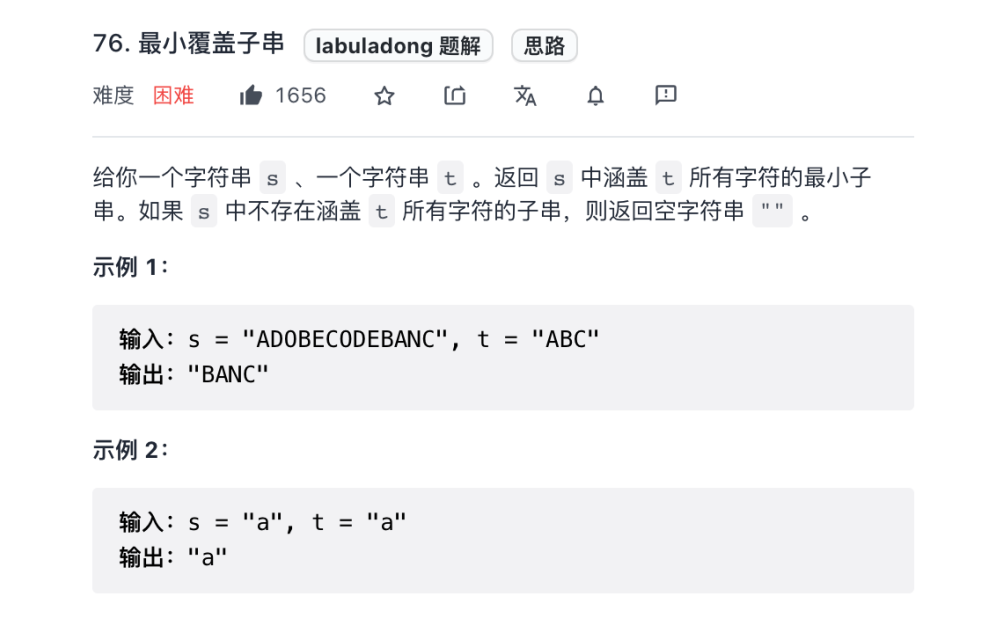
/**
* 求字符串 s 中包含字符串 t 所有字符的最小子串
* @param s 源字符串
* @param t 给定字符串
* @return 满足条件的最小子串
*/
public String minWindow(String s, String t) {
// 用于记录需要的字符和窗口中的字符及其出现的次数
Map<Character, Integer> need = new HashMap<>();
Map<Character, Integer> window = new HashMap<>();
// 统计 t 中各字符出现次数
for (char c : t.toCharArray())
need.put(c, need.getOrDefault(c, 0) + 1);
int left = 0, right = 0;
int valid = 0; // 窗口中满足需要的字符个数
// 记录最小覆盖子串的起始索引及长度
int start = 0, len = Integer.MAX_VALUE;
while (right < s.length()) {
// c 是将移入窗口的字符
char c = s.charAt(right);
// 扩大窗口
right++;
// 进行窗口内数据的一系列更新
if (need.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
if (window.get(c).equals(need.get(c)))
valid++; // 只有当 window[c] 和 need[c] 对应的出现次数一致时,才能满足条件,valid 才能 +1
}
// 判断左侧窗口是否要收缩
while (valid == need.size()) {
// 更新最小覆盖子串
if (right - left < len) {
start = left;
len = right - left;
}
// d 是将移出窗口的字符
char d = s.charAt(left);
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
if (need.containsKey(d)) {
if (window.get(d).equals(need.get(d)))
valid--; // 只有当 window[d] 内的出现次数和 need[d] 相等时,才能 -1
window.put(d, window.get(d) - 1);
}
}
}
// 返回最小覆盖子串
return len == Integer.MAX_VALUE ?
"" : s.substring(start, start + len);
}
(2) 最小异位词

public List<Integer> findAnagrams(String s, String t) {
Map<Character, Integer> need = new HashMap<>();
Map<Character, Integer> window = new HashMap<>();
for (int i = 0; i < t.length(); i++) {
char c = t.charAt(i);
need.put(c, need.getOrDefault(c, 0) + 1);
}
int left = 0, right = 0;
int valid = 0;
List<Integer> res = new ArrayList<>(); // 记录结果
while (right < s.length()) {
char c = s.charAt(right);
right++;
// 进行窗口内数据的一系列更新
if (need.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
if (window.get(c).equals(need.get(c))) {
valid++;
}
}
// 判断左侧窗口是否要收缩
while (right - left >= t.length()) {
// 当窗口符合条件时,把起始索引加入 res
if (valid == need.size()) {
res.add(left);
}
char d = s.charAt(left);
left++;
// 进行窗口内数据的一系列更新
if (need.containsKey(d)) {
if (window.get(d).equals(need.get(d))) {
valid--;
}
window.put(d, window.get(d) - 1);
}
}
}
return res;
}
另一种滑动窗口算法
模板
def findSubArray(nums):
N = len(nums) # 数组/字符串长度
left, right = 0, 0 # 双指针,表示当前遍历的区间[left, right],闭区间
sums = 0 # 用于统计 子数组/子区间 是否有效,根据题目可能会改成求和/计数
res = 0 # 保存最大的满足题目要求的 子数组/子串 长度
while right < N: # 当右边的指针没有搜索到 数组/字符串 的结尾
sums += nums[right] # 增加当前右边指针的数字/字符的求和/计数
while 区间[left, right]不符合题意: # 此时需要一直移动左指针,直至找到一个符合题意的区间
sums -= nums[left] # 移动左指针前需要从counter中减少left位置字符的求和/计数
left += 1 # 真正的移动左指针,注意不能跟上面一行代码写反
# 到 while 结束时,我们找到了一个符合题意要求的 子数组/子串
res = max(res, right - left + 1) # 需要更新结果
right += 1 # 移动右指针,去探索新的区间
return res
最大连续1个数

class Solution {
public int longestOnes(int[] A, int K) {
int N = A.length;
int res = 0;
int left = 0, right = 0;
int zeros = 0;
while (right < N) {
if (A[right] == 0)
zeros ++;
while (zeros > K) {
if (A[left++] == 0)
zeros --;
}
res = Math.max(res, right - left + 1);
right ++;
}
return res;
}
}
反转链表
class Solution {
public ListNode reverseList(ListNode head) {
ListNode prev = null;
ListNode curr = head;
while(curr != null) {
ListNode nxt = curr.next;
curr.next = prev; // 翻转箭头
prev = curr; //三人行
curr = nxt; //三人行
}
return prev;
}
}

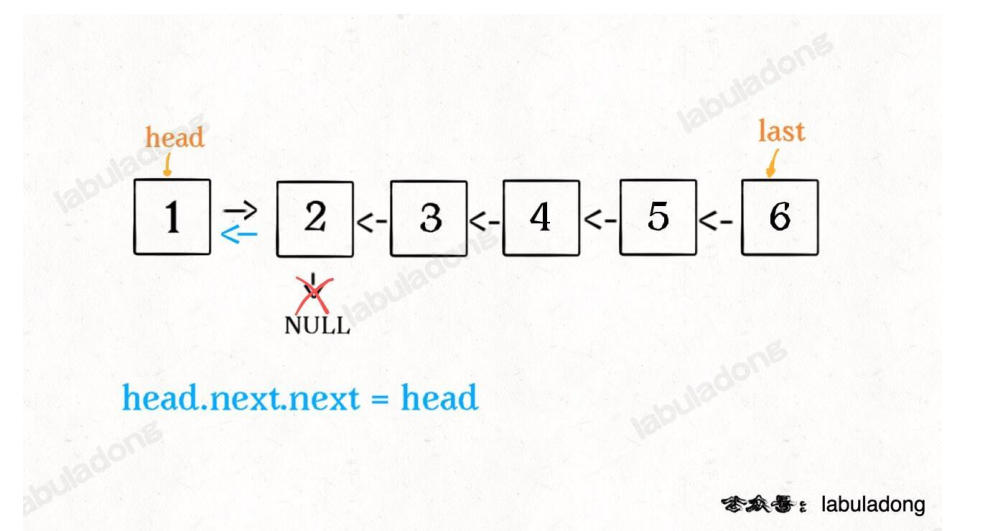
(1)反转链表前N个节点
ListNode successor = null; // 后驱节点
// 反转以 head 为起点的 n 个节点,返回新的头结点
ListNode reverseN(ListNode head, int n) {
if (n == 1) {
// 记录第 n + 1 个节点
successor = head.next;
return head;
}
// 以 head.next 为起点,需要反转前 n - 1 个节点
ListNode last = reverseN(head.next, n - 1);
head.next.next = head;
// 让反转之后的 head 节点和后⾯的节点连起来
head.next = successor;
return last;
}
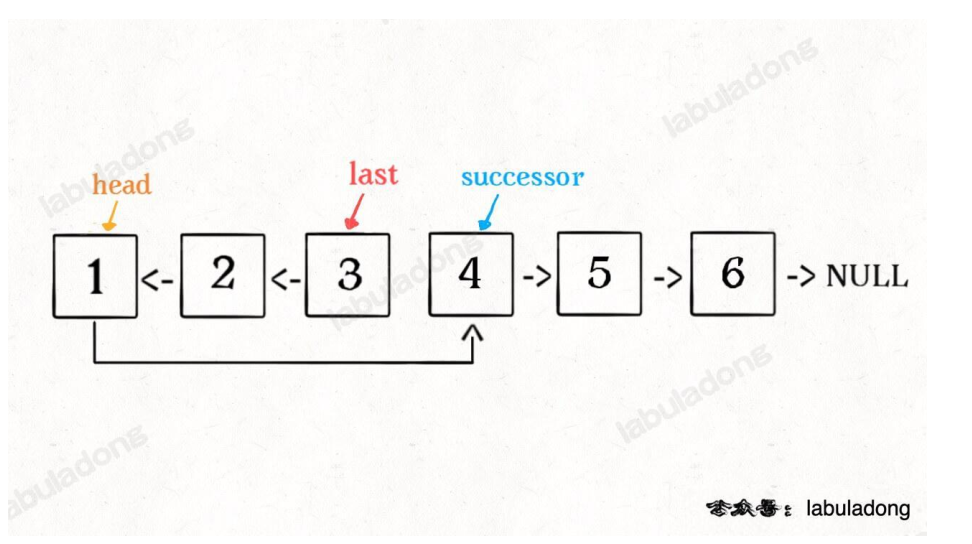
(2)反转链表的一部分
ListNode reverseBetween(ListNode head, int m, int n) {
// base case
if (m == 1) {
return reverseN(head, n);
}
// 前进到反转的起点触发 base case
head.next = reverseBetween(head.next, m - 1, n - 1);
return head;
}
单调栈

int[] nextGreaterElement(int[] nums1, int[] nums2) {
// 记录 nums2 中每个元素的下一个更大元素
int[] greater = nextGreaterElement(nums2);
// 转化成映射:元素 x -> x 的下一个最大元素
HashMap<Integer, Integer> greaterMap = new HashMap<>();
for (int i = 0; i < nums2.length; i++) {
greaterMap.put(nums2[i], greater[i]);
}
// nums1 是 nums2 的子集,所以根据 greaterMap 可以得到结果
int[] res = new int[nums1.length];
for (int i = 0; i < nums1.length; i++) {
res[i] = greaterMap.get(nums1[i]);
}
return res;
}
int[] nextGreaterElement(int[] nums) {
int n = nums.length;
// 存放答案的数组
int[] res = new int[n];
Stack<Integer> s = new Stack<>();
// 倒着往栈里放
for (int i = n - 1; i >= 0; i--) {
// 判定个子高矮
while (!s.isEmpty() && s.peek() <= nums[i]) {
// 矮个起开,反正也被挡着了。。。
s.pop();
}
// nums[i] 身后的更大元素
res[i] = s.isEmpty() ? -1 : s.peek();
s.push(nums[i]);
}
return res;
}
二叉树
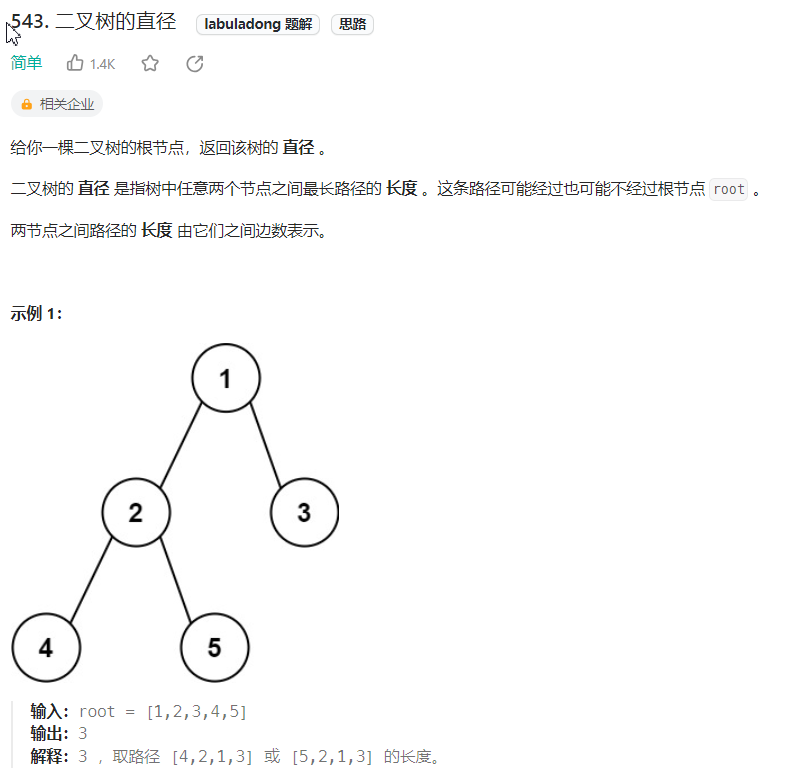
(1) 二叉树的直径
class Solution {
// 记录最大直径的长度
int maxDiameter = 0;
public int diameterOfBinaryTree(TreeNode root) {
// 对每个节点计算直径,求最大直径
traverse(root);
return maxDiameter;
}
// 遍历二叉树
void traverse(TreeNode root) {
if (root == null) {
return;
}
// 对每个节点计算直径
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
int myDiameter = leftMax + rightMax;
// 更新全局最大直径
maxDiameter = Math.max(maxDiameter, myDiameter);
traverse(root.left);
traverse(root.right);
}
// 计算二叉树的最大深度
int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
return 1 + Math.max(leftMax, rightMax);
}
}
(2)层序遍历
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
if (root != null) queue.add(root);
while (!queue.isEmpty()) {
List<Integer> tmp = new ArrayList<>();
for(int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
tmp.add(node.val);
if (node.left != null) queue.add(node.left);
if (node.right != null) queue.add(node.right);
}
res.add(tmp);
}
return res;
}
}
二叉树解题的思维模式分两类:
1、是否可以通过遍历一遍二叉树得到答案?如果可以,用一个 traverse 函数配合外部变量来实现,这叫「遍历」的思维模式。
2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。
无论使用哪种思维模式,你都需要思考:
如果单独抽出一个二叉树节点,它需要做什么事情?需要在什么时候(前/中/后序位置)做?其他的节点不用你操心,递归函数会帮你在所有节点上执行相同的操作。
(3)翻转二叉树
// 主函数
TreeNode invertTree(TreeNode root) {
// 遍历二叉树,交换每个节点的子节点
traverse(root);
return root;
}
// 二叉树遍历函数
void traverse(TreeNode root) {
if (root == null) {
return;
}
/**** 前序位置 ****/
// 每一个节点需要做的事就是交换它的左右子节点
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
// 遍历框架,去遍历左右子树的节点
traverse(root.left);
traverse(root.right);
}
(4)二叉树展开为链表
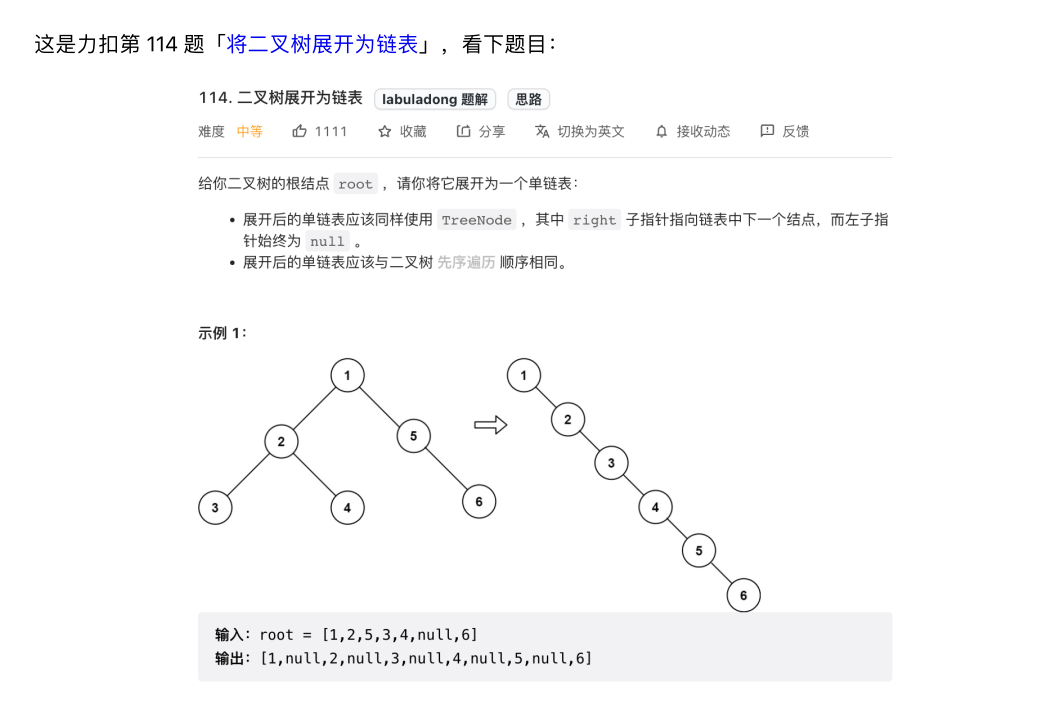
你看,这就是递归的魅力,你说 flatten 函数是怎么把左右子树拉平的?
不容易说清楚,但是只要知道 flatten 的定义如此并利用这个定义,让每一个节点做它该做的事情,然后 flatten 函数就会按照定义工作。
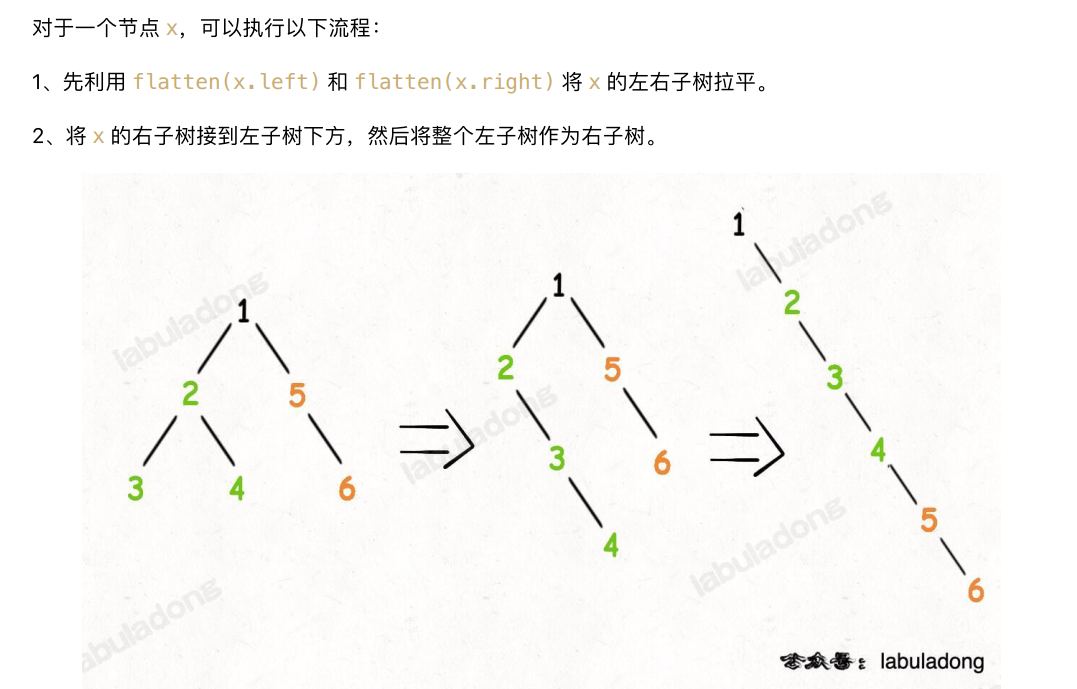
// 定义:将以 root 为根的树拉平为链表
void flatten(TreeNode root) {
// base case
if (root == null) return;
// 利用定义,把左右子树拉平
flatten(root.left);
flatten(root.right);
/**** 后序遍历位置 ****/
// 1、左右子树已经被拉平成一条链表
TreeNode left = root.left;
TreeNode right = root.right;
// 2、将左子树作为右子树
root.left = null;
root.right = left;
// 3、将原先的右子树接到当前右子树的末端
TreeNode p = root;
while (p.right != null) {
p = p.right;
}
p.right = right;
}
(5)最大二叉树

/* 主函数 */
TreeNode constructMaximumBinaryTree(int[] nums) {
return build(nums, 0, nums.length - 1);
}
// 定义:将 nums[lo..hi] 构造成符合条件的树,返回根节点
TreeNode build(int[] nums, int lo, int hi) {
// base case
if (lo > hi) {
return null;
}
// 找到数组中的最大值和对应的索引
int index = -1, maxVal = Integer.MIN_VALUE;
for (int i = lo; i <= hi; i++) {
if (maxVal < nums[i]) {
index = i;
maxVal = nums[i];
}
}
// 先构造出根节点
TreeNode root = new TreeNode(maxVal);
// 递归调用构造左右子树
root.left = build(nums, lo, index - 1);
root.right = build(nums, index + 1, hi);
return root;
}
(6) 二叉树重复子树
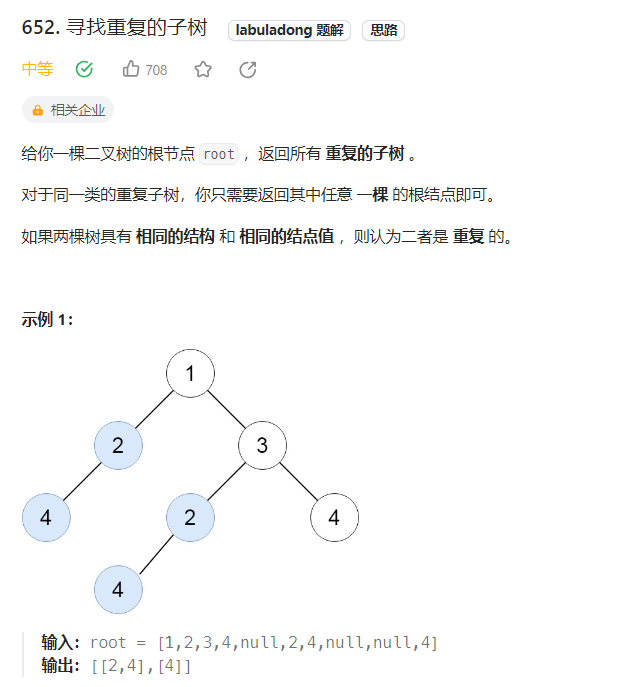
class Solution {
Map<String, Integer> map = new HashMap<>();
List<TreeNode> ans = new ArrayList<>();
public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
dfs(root);
return ans;
}
String dfs(TreeNode root) {
if (root == null) return " ";
StringBuilder sb = new StringBuilder();
sb.append(root.val).append("_");
sb.append(dfs(root.left)).append(dfs(root.right));
String key = sb.toString();
map.put(key, map.getOrDefault(key, 0) + 1);
if (map.get(key) == 2) ans.add(root);
return key;
}
}
DFS/回溯算法
(1) 全排列

class Solution {
List<List<Integer>> res = new LinkedList<>();
/* 主函数,输入一组不重复的数字,返回它们的全排列 */
List<List<Integer>> permute(int[] nums) {
// 记录「路径」
LinkedList<Integer> track = new LinkedList<>();
// 「路径」中的元素会被标记为 true,避免重复使用
boolean[] used = new boolean[nums.length];
backtrack(nums, track, used);
return res;
}
// 路径:记录在 track 中
// 选择列表:nums 中不存在于 track 的那些元素(used[i] 为 false)
// 结束条件:nums 中的元素全都在 track 中出现
void backtrack(int[] nums, LinkedList<Integer> track, boolean[] used) {
// 触发结束条件
if (track.size() == nums.length) {
res.add(new LinkedList(track));
return;
}
for (int i = 0; i < nums.length; i++) {
// 排除不合法的选择
if (used[i]) {
// nums[i] 已经在 track 中,跳过
continue;
}
// 做选择
track.add(nums[i]);
used[i] = true;
// 进入下一层决策树
backtrack(nums, track, used);
// 取消选择
track.removeLast();
used[i] = false;
}
}
}
(2) 子集、组合问题
(1)子集 力扣第 78 题「子集」就是这个问题:
题目给你输入一个无重复元素的数组 nums,其中每个元素最多使用一次,请你返回 nums 的所有子集。
比如输入 nums = [1,2,3],算法应该返回如下子集:
[ [],[1],[2],[3],[1,2],[1,3],[2,3],[1,2,3] ]
class Solution {
List<List<Integer>> res = new LinkedList<>();
// 记录回溯算法的递归路径
LinkedList<Integer> track = new LinkedList<>();
// 主函数
public List<List<Integer>> subsets(int[] nums) {
backtrack(nums, 0);
return res;
}
// 回溯算法核心函数,遍历子集问题的回溯树
void backtrack(int[] nums, int start) {
// 前序位置,每个节点的值都是一个子集
res.add(new LinkedList<>(track));
// 回溯算法标准框架
for (int i = start; i < nums.length; i++) {
// 做选择
track.addLast(nums[i]);
// 通过 start 参数控制树枝的遍历,避免产生重复的子集
backtrack(nums, i + 1);
// 撤销选择
track.removeLast();
}
}
}
(2) 组合 比如 combine(3, 2) 的返回值应该是:
[ [1,2],[1,3],[2,3] ]
class Solution {
List<List<Integer>> res = new LinkedList<>();
// 记录回溯算法的递归路径
LinkedList<Integer> track = new LinkedList<>();
// 主函数
public List<List<Integer>> combine(int n, int k) {
backtrack(1, n, k);
return res;
}
void backtrack(int start, int n, int k) {
// base case
if (k == track.size()) {
// 遍历到了第 k 层,收集当前节点的值
res.add(new LinkedList<>(track));
return;
}
// 回溯算法标准框架
for (int i = start; i <= n; i++) {
// 选择
track.addLast(i);
// 通过 start 参数控制树枝的遍历,避免产生重复的子集
backtrack(i + 1, n, k);
// 撤销选择
track.removeLast();
}
}
}
(3) 重复元素的子集和组合
比如输入 nums = [1,2,2],你应该输出:
[ [],[1],[2],[1,2],[2,2],[1,2,2] ]
class Solution {
List<List<Integer>> res = new LinkedList<>();
LinkedList<Integer> track = new LinkedList<>();
public List<List<Integer>> subsetsWithDup(int[] nums) {
// 先排序,让相同的元素靠在一起
Arrays.sort(nums);
backtrack(nums, 0);
return res;
}
void backtrack(int[] nums, int start) {
// 前序位置,每个节点的值都是一个子集
res.add(new LinkedList<>(track));
for (int i = start; i < nums.length; i++) {
// 剪枝逻辑,值相同的相邻树枝,只遍历第一条
if (i > start && nums[i] == nums[i - 1]) {
continue;
}
track.addLast(nums[i]);
backtrack(nums, i + 1);
track.removeLast();
}
}
}
BFS算法
(1) 打开密码盘的最少次数

String plusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == '9')
ch[j] = '0';
else
ch[j] += 1;
return new String(ch);
}
// 将 s[i] 向下拨动一次
String minusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == '0')
ch[j] = '9';
else
ch[j] -= 1;
return new String(ch);
}
int openLock(String[] deadends, String target) {
// 记录需要跳过的死亡密码
Set<String> deads = new HashSet<>();
for (String s : deadends) deads.add(s);
// 记录已经穷举过的密码,防止走回头路
Set<String> visited = new HashSet<>();
Queue<String> q = new LinkedList<>();
// 从起点开始启动广度优先搜索
int step = 0;
q.offer("0000");
visited.add("0000");
while (!q.isEmpty()) {
int sz = q.size();
/* 将当前队列中的所有节点向周围扩散 */
for (int i = 0; i < sz; i++) {
String cur = q.poll();
/* 判断是否到达终点 */
if (deads.contains(cur))
continue;
if (cur.equals(target))
return step;
/* 将一个节点的未遍历相邻节点加入队列 */
for (int j = 0; j < 4; j++) {
String up = plusOne(cur, j);
if (!visited.contains(up)) {
q.offer(up);
visited.add(up);
}
String down = minusOne(cur, j);
if (!visited.contains(down)) {
q.offer(down);
visited.add(down);
}
}
}
/* 在这里增加步数 */
step++;
}
// 如果穷举完都没找到目标密码,那就是找不到了
return -1;
}
(2) 滑动谜题

class Solution {
public int slidingPuzzle(int[][] board) {
int m = 2, n = 3;
StringBuilder sb = new StringBuilder();
String target = "123450";
// 将 2x3 的数组转化成字符串作为 BFS 的起点
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
sb.append(board[i][j]);
}
}
String start = sb.toString();
// 记录一维字符串的相邻索引
int[][] neighbor = new int[][]{
{1, 3},
{0, 4, 2},
{1, 5},
{0, 4},
{3, 1, 5},
{4, 2}
};
/******* BFS 算法框架开始 *******/
Queue<String> q = new LinkedList<>();
HashSet<String> visited = new HashSet<>();
// 从起点开始 BFS 搜索
q.offer(start);
visited.add(start);
int step = 0;
while (!q.isEmpty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
String cur = q.poll();
// 判断是否达到目标局面
if (target.equals(cur)) {
return step;
}
// 找到数字 0 的索引
int idx = 0;
for (; cur.charAt(idx) != '0'; idx++) ;
// 将数字 0 和相邻的数字交换位置
for (int adj : neighbor[idx]) {
String new_board = swap(cur.toCharArray(), adj, idx);
// 防止走回头路
if (!visited.contains(new_board)) {
q.offer(new_board);
visited.add(new_board);
}
}
}
step++;
}
/******* BFS 算法框架结束 *******/
return -1;
}
private String swap(char[] chars, int i, int j) {
char temp = chars[i];
chars[i] = chars[j];
chars[j] = temp;
return new String(chars);
}
}
动态规划
(1) 凑零钱
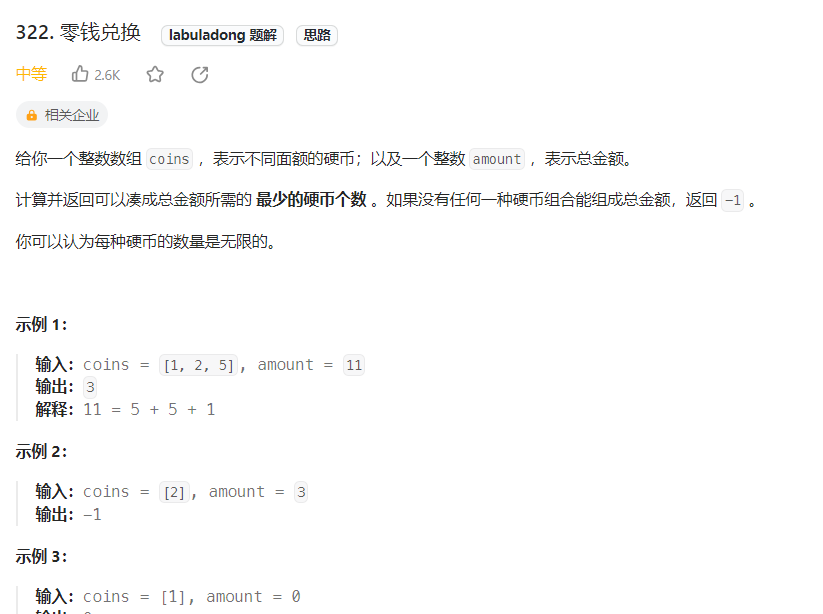
class Solution {
int[] memo;
int coinChange(int[] coins, int amount) {
memo = new int[amount + 1];
// 备忘录初始化为一个不会被取到的特殊值,代表还未被计算
Arrays.fill(memo, -666);
return dp(coins, amount);
}
int dp(int[] coins, int amount) {
if (amount == 0) return 0;
if (amount < 0) return -1;
// 查备忘录,防止重复计算
if (memo[amount] != -666)
return memo[amount];
int res = Integer.MAX_VALUE;
for (int coin : coins) {
// 计算子问题的结果
int subProblem = dp(coins, amount - coin);
// 子问题无解则跳过
if (subProblem == -1) continue;
// 在子问题中选择最优解,然后加一
res = Math.min(res, subProblem + 1);
}
// 把计算结果存入备忘录
memo[amount] = (res == Integer.MAX_VALUE) ? -1 : res;
return memo[amount];
}
}
(2) 下降路径最小和

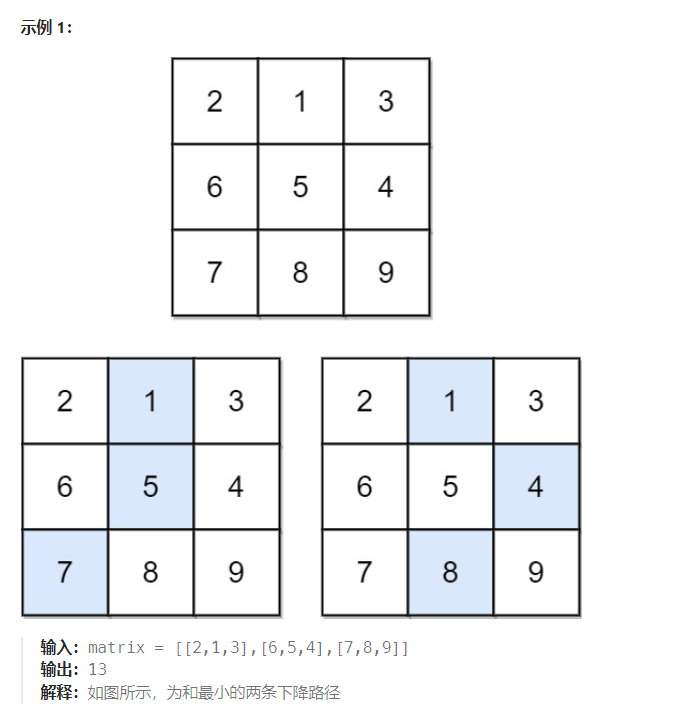
class Solution {
int minFallingPathSum(int[][] matrix) {
int n = matrix.length;
int res = Integer.MAX_VALUE;
// 备忘录里的值初始化为 66666
memo = new int[n][n];
for (int i = 0; i < n; i++) {
Arrays.fill(memo[i], 66666);
}
// 终点可能在 matrix[n-1] 的任意一列
for (int j = 0; j < n; j++) {
res = Math.min(res, dp(matrix, n - 1, j));
}
return res;
}
// 备忘录
int[][] memo;
int dp(int[][] matrix, int i, int j) {
// 1、索引合法性检查
if (i < 0 || j < 0 ||
i >= matrix.length ||
j >= matrix[0].length) {
return 99999;
}
// 2、base case
if (i == 0) {
return matrix[0][j];
}
// 3、查找备忘录,防止重复计算
if (memo[i][j] != 66666) {
return memo[i][j];
}
// 进行状态转移
memo[i][j] = matrix[i][j] + min(
dp(matrix, i - 1, j),
dp(matrix, i - 1, j - 1),
dp(matrix, i - 1, j + 1)
);
return memo[i][j];
}
int min(int a, int b, int c) {
return Math.min(a, Math.min(b, c));
}
}
(3) 不同的子序列

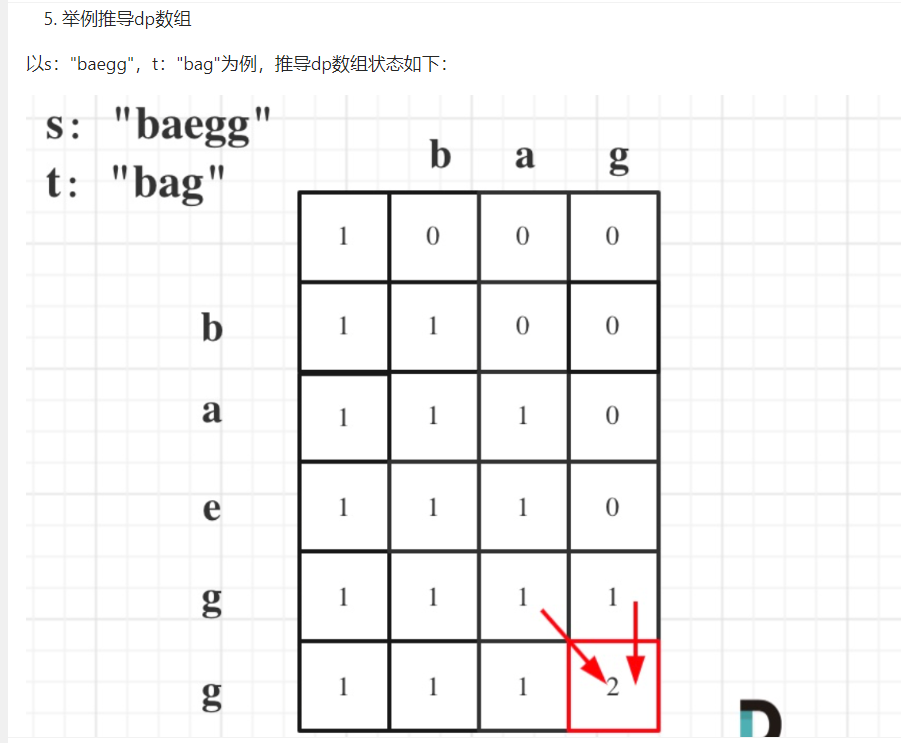
class Solution {
public int numDistinct(String s, String t) {
int[][] dp = new int[s.length() + 1][t.length() + 1];
for (int i = 0; i < s.length() + 1; i++) {
dp[i][0] = 1;
}
for (int i = 1; i < s.length() + 1; i++) {
for (int j = 1; j < t.length() + 1; j++) {
if (s.charAt(i - 1) == t.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
}else{
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[s.length()][t.length()];
}
}
or
class Solution2 {
int[][] memo;
int numDistinct(String s, String t) {
// 初始化备忘录为特殊值 -1
memo = new int[s.length()][t.length()];
for (int[] row : memo) {
Arrays.fill(row, -1);
}
return dp(s, 0, t, 0);
}
// 定义:s[i..] 的⼦序列中 t[j..] 出现的次数为 dp(s, i, t, j)
int dp(String s, int i, String t, int j) {
// base case 1
if (j == t.length()) {
return 1;
}
// base case 2
if (s.length() - i < t.length() - j) {
return 0;
}
// 查备忘录防⽌冗余计算
if (memo[i][j] != -1) {
return memo[i][j];
}
int res = 0;
// 执⾏状态转移⽅程
if (s.charAt(i) == t.charAt(j)) {
// 匹配,两种情况,累加关系
res += dp(s, i + 1, t, j + 1) + dp(s, i + 1, t, j);
} else {
// 不匹配,在 s[i+1..] 的⼦序列中计算 t[j..] 的出现次数
res += dp(s, i + 1, t, j);
}
// 结果存⼊备忘录
memo[i][j] = res;
return res;
}
}
(4) 最长递增子序列

int lengthOfLIS(int[] nums) {
// 定义:dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度
int[] dp = new int[nums.length];
// base case:dp 数组全都初始化为 1
Arrays.fill(dp, 1);
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j])
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
int res = 0;
for (int i = 0; i < dp.length; i++) {
res = Math.max(res, dp[i]);
}
return res;
}
(5) 俄罗斯信封套娃

// envelopes = [[w, h], [w, h]...]
public int maxEnvelopes(int[][] envelopes) {
int n = envelopes.length;
// 按宽度升序排列,如果宽度一样,则按高度降序排列
Arrays.sort(envelopes, new Comparator<int[]>()
{
public int compare(int[] a, int[] b) {
return a[0] == b[0] ?
b[1] - a[1] : a[0] - b[0];
}
});
// 对高度数组寻找 LIS
int[] height = new int[n];
for (int i = 0; i < n; i++)
height[i] = envelopes[i][1];
return lengthOfLIS(height);
}
int lengthOfLIS(int[] nums) {
// 见前文
}
(6) 最大子数组和

int maxSubArray(int[] nums) {
int n = nums.length;
if (n == 0) return 0;
// 定义:dp[i] 记录以 nums[i] 为结尾的「最大子数组和」
int[] dp = new int[n];
// base case
// 第一个元素前面没有子数组
dp[0] = nums[0];
// 状态转移方程
for (int i = 1; i < n; i++) {
dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
}
// 得到 nums 的最大子数组
int res = Integer.MIN_VALUE;
for (int i = 0; i < n; i++) {
res = Math.max(res, dp[i]);
}
return res;
}
(7) 编辑距离

class Solution {
// 备忘录
int[][] memo;
public int minDistance(String s1, String s2) {
int m = s1.length(), n = s2.length();
// 备忘录初始化为特殊值,代表还未计算
memo = new int[m][n];
for (int[] row : memo) {
Arrays.fill(row, -1);
}
return dp(s1, m - 1, s2, n - 1);
}
int dp(String s1, int i, String s2, int j) {
if (i == -1) return j + 1;
if (j == -1) return i + 1;
// 查备忘录,避免重叠子问题
if (memo[i][j] != -1) {
return memo[i][j];
}
// 状态转移,结果存入备忘录
if (s1.charAt(i) == s2.charAt(j)) {
memo[i][j] = dp(s1, i - 1, s2, j - 1);
} else {
memo[i][j] = min(
dp(s1, i, s2, j - 1) + 1,
dp(s1, i - 1, s2, j) + 1,
dp(s1, i - 1, s2, j - 1) + 1
);
}
return memo[i][j];
}
int min(int a, int b, int c) {
return Math.min(a, Math.min(b, c));
}
}
(8) 最长公共子序列

class Solution {
// 备忘录
int[][] memo;
public int longestCommonSubsequence(String s1, String s2) {
int m = s1.length(), n = s2.length();
// 备忘录初始化为特殊值,代表还未计算
memo = new int[m][n];
for (int[] row : memo) {
Arrays.fill(row, -1);
}
return dp(s1, 0, s2, 0);
}
int dp(String s1, int i, String s2, int j) {
if (i == s1.length() || j == s2.length())
return 0;
// 查备忘录,避免重叠子问题
if (memo[i][j] != -1) {
return memo[i][j];
}
// 状态转移,结果存入备忘录
if (s1.charAt(i) == s2.charAt(j)) {
memo[i][j] = dp(s1, i + 1, s2, j + 1) + 1;
} else {
memo[i][j] = Math.max(
dp(s1, i + 1, s2, j),
dp(s1, i, s2, j +1 )
);
}
return memo[i][j];
}
}
(8)II 最长公共子串
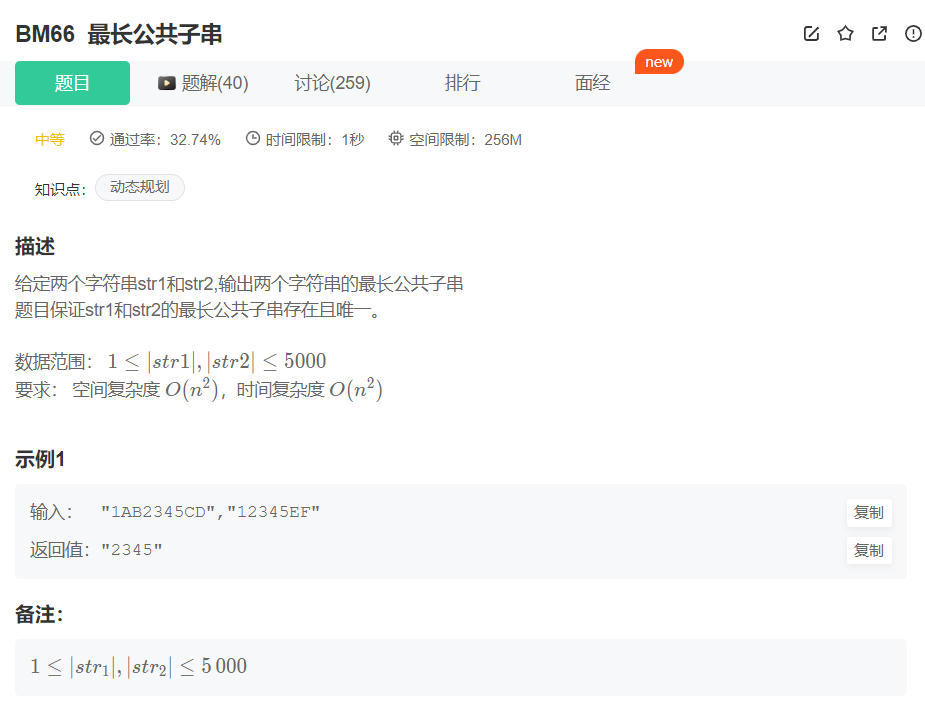
定义dp[i][j]表示字符串str1中第i个字符和str2种第j个字符为最后一个元素所构成的最长公共子串。如果要求dp[i][j],也就是str1的第i个字符和str2的第j个字符为最后一个元素所构成的最长公共子串,我们首先需要判断这两个字符是否相等。
-
如果不相等,那么他们就不能构成公共子串,也就是
dp[i][j]=0; -
如果相等,我们还需要计算前面相等字符的个数,其实就是dp[i-1][j-1],所以
dp[i][j]=dp[i-1][j-1]+1;
public String LCS(String str1, String str2) {
int maxLenth = 0;//记录最长公共子串的长度
//记录最长公共子串最后一个元素在字符串str1中的位置
int maxLastIndex = 0;
int[][] dp = new int[str1.length() + 1][str2.length() + 1];
for (int i = 0; i < str1.length(); i++) {
for (int j = 0; j < str2.length(); j++) {
//递推公式,两个字符相等的情况
if (str1.charAt(i) == str2.charAt(j)) {
dp[i + 1][j + 1] = dp[i][j] + 1;
//如果遇到了更长的子串,要更新,记录最长子串的长度,
//以及最长子串最后一个元素的位置
if (dp[i + 1][j + 1] > maxLenth) {
maxLenth = dp[i + 1][j+1];
maxLastIndex = i;
}
} else {
//递推公式,两个字符不相等的情况
dp[i + 1][j+1] = 0;
}
}
}
//最字符串进行截取,substring(a,b)中a和b分别表示截取的开始和结束位置
return str1.substring(maxLastIndex - maxLenth + 1, maxLastIndex + 1);
}
(9) 填满背包的最大价值
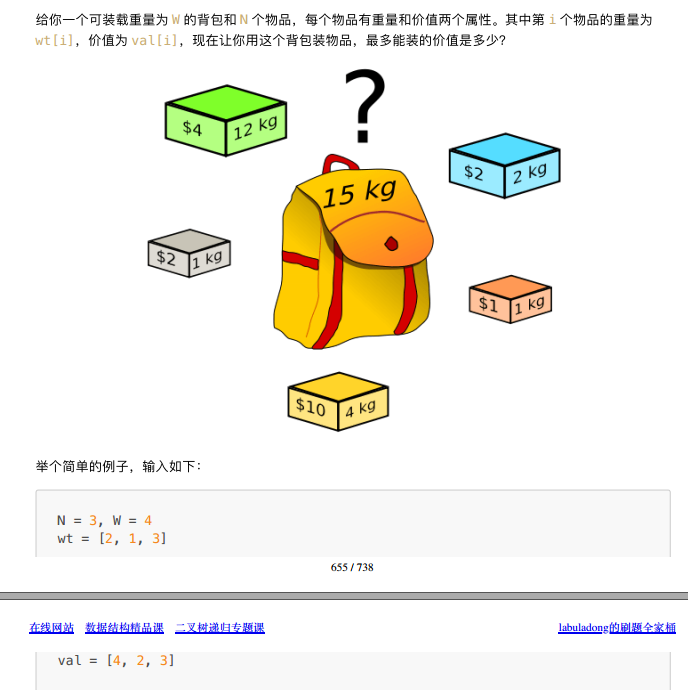
int knapsack(int W, int N, int[] wt, int[] val) {
assert N == wt.length;
// base case 已初始化
int[][] dp = new int[N + 1][W + 1];
for (int i = 1; i <= N; i++) {
for (int w = 1; w <= W; w++) {
if (w - wt[i - 1] < 0) {
// 这种情况下只能选择不装入背包
dp[i][w] = dp[i - 1][w];
} else {
// 装入或者不装入背包,择优
dp[i][w] = Math.max(
dp[i - 1][w - wt[i-1]] + val[i-1],
dp[i - 1][w]
);
}
}
}
return dp[N][W];
}
(10) 完全背包问题

dp[i][j] 的定义如下:
若只使用前 i 个物品(可以重复使用),当背包容量为 j 时,有 dp[i][j] 种方法可以装满背包。
换句话说,翻译回我们题目的意思就是:
若只使用 coins 中的前 i 个(i 从 1 开始计数)硬币的面值,若想凑出金额 j,有 dp[i][j] 种凑法。
int change(int amount, int[] coins) {
int n = coins.length;
int[][] dp = int[n + 1][amount + 1];
// base case
for (int i = 0; i <= n; i++)
dp[i][0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= amount; j++)
if (j - coins[i-1] >= 0)
dp[i][j] = dp[i - 1][j]
+ dp[i][j - coins[i-1]];
else
dp[i][j] = dp[i - 1][j];
}
return dp[n][amount];
}
而且,我们通过观察可以发现,dp 数组的转移只和 dp[i][..] 和 dp[i-1][..] 有关,所以可以使用前文讲的 动态规划空间压缩技巧,进一步降低算法的空间复杂度:
int change(int amount, int[] coins) {
int n = coins.length;
int[] dp = new int[amount + 1];
dp[0] = 1; // base case
for (int i = 0; i < n; i++)
for (int j = 1; j <= amount; j++)
if (j - coins[i] >= 0)
dp[j] = dp[j] + dp[j-coins[i]];
return dp[amount];
}
(11) 分割等和子集

目标的一半,从原来挑选一些元素目标和的一半,剩下的肯定也是一半
boolean canPartition(int[] nums) {
int sum = 0;
for (int num : nums) sum += num;
// 和为奇数时,不可能划分成两个和相等的集合
if (sum % 2 != 0) return false;
int n = nums.length;
sum = sum / 2;
boolean[][] dp = new boolean[n + 1][sum + 1];
// base case
for (int i = 0; i <= n; i++)
dp[i][0] = true;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= sum; j++) {
if (j - nums[i - 1] < 0) {
// 背包容量不足,不能装入第 i 个物品
dp[i][j] = dp[i - 1][j];
} else {
// 装入或不装入背包
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];
}
}
}
return dp[n][sum];
}
or
boolean canPartition(int[] nums) {
int sum = 0;
for (int num : nums) sum += num;
// 和为奇数时,不可能划分成两个和相等的集合
if (sum % 2 != 0) return false;
int n = nums.length;
sum = sum / 2;
boolean[] dp = new boolean[sum + 1];
// base case
dp[0] = true;
for (int i = 0; i < n; i++) {
for (int j = sum; j >= 0; j--) {
if (j - nums[i] >= 0) {
dp[j] = dp[j] || dp[j - nums[i]];
}
}
}
return dp[sum];
}
